Statystyki - odwrotna dystrybucja gamma
Odwrotny rozkład gamma jest odwrotnością funkcji gęstości prawdopodobieństwa gamma z dodatnimi parametrami kształtu $ {\ alpha, \ beta} $ i parametrem lokalizacji $ {\ mu} $. $ {\ alpha} $ kontroluje wysokość. Wyższa wartość $ {\ alpha} $, tym wyższa funkcja gęstości prawdopodobieństwa (PDF). $ {\ beta} $ kontroluje prędkość. Określa ją następujący wzór.
Formuła
$ {f (x) = \ frac {x ^ {- (\ alpha + 1)} e ^ {\ frac {-1} {\ beta x}}} {\ Gamma (\ alpha) \ beta ^ \ alpha} \\ [7pt] \, gdzie x \ gt 0} $
Gdzie -
$ {\ alpha} $ = dodatni parametr kształtu.
$ {\ beta} $ = dodatni parametr kształtu.
$ {x} $ = zmienna losowa.
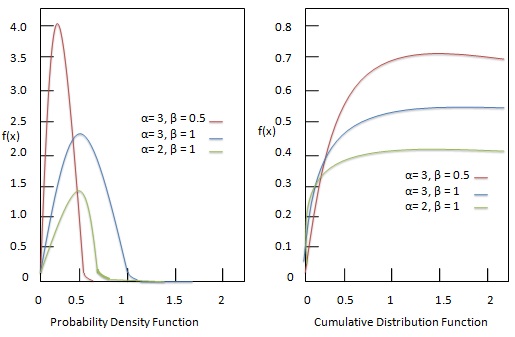
Poniższy diagram przedstawia funkcję gęstości prawdopodobieństwa z różnymi kombinacjami parametrów.