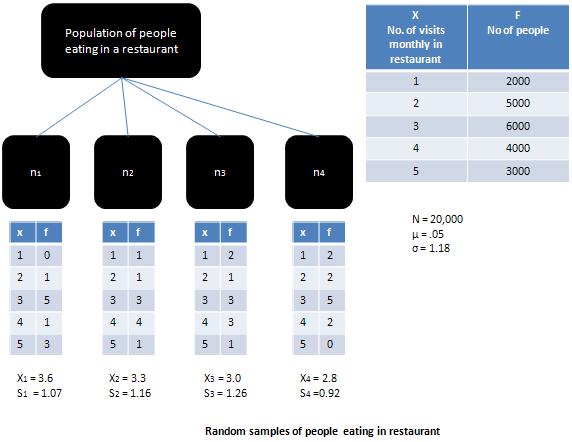
Statystyka - centralne twierdzenie graniczne
Jeśli populacja, z której pobrano próbkę, jest populacją normalną, wówczas sample means byłaby równa średniej populacji i sampling distributionbyłoby normalne. Gdy większa populacja jest wypaczona, jak pokazano na rysunku, wówczassampling distribution miałby tendencję do zbliżania się do rozkładu normalnego, pod warunkiem, że próbka jest duża (tj. większa niż 30).
Według Central Limit Theorem, dla wystarczająco dużych próbek o rozmiarze większym niż 30, kształt sampling distribution będzie coraz bardziej przypominać plik normal distributionniezależnie od kształtu populacji rodziców. To twierdzenie wyjaśnia związek międzypopulation distribution i sampling distribution. Podkreśla fakt, że jeśli istnieje wystarczająco duży zestaw próbek, wówczas pliksampling distribution średnich podejść normal distribution. Znaczenie centralnego twierdzenia granicznego zostało podsumowane przez Richarda. I. Levin następującymi słowami:
Znaczenie centralnego twierdzenia granicznego polega na tym, że pozwala nam ono na wykorzystanie statystyk próbnych do wnioskowania o parametrach populacji bez wiedzy o kształcie rozkładu częstotliwości tej populacji, poza tym, co możemy uzyskać z próby.