Statystyka - porównanie wykresów
Grupy ludności można porównać, korzystając z wykresów pudełkowych i wąsów. Ogólny widoczny spread i różnica między medianą służy do wyciągania wniosku, że między dwiema grupami występuje różnica lub nie.
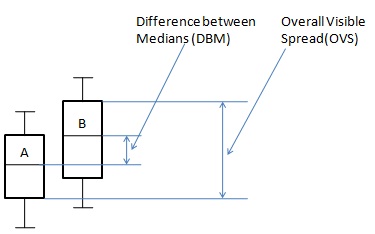
Przypadek 2: Formuła
$ {P = \ frac {DBM} {OVS} \ times 100} $
Gdzie -
{P} zł = różnica procentowa
$ {DBM} $ = różnica między medianami.
$ {OVS} $ = Ogólny widoczny spread.
Zasady
W przypadku próby liczącej 30 osób, jeśli odsetek ten jest większy niż 33%, zwykle występuje różnica między dwiema grupami.
W przypadku liczebności próby 100, jeśli odsetek ten jest większy niż 20%, zwykle występuje różnica między dwiema grupami.
W przypadku próby liczącej 1000 osób, jeśli odsetek ten jest większy niż 10%, zwykle występuje różnica między dwiema grupami.
Przykład
Oświadczenie dotyczące problemu:
Opisz różnicę między następującymi zestawami danych.
| Sr. No. | Nazwa | Zestaw A | Zestaw B. |
|---|---|---|---|
| 1 | Maks | 12 | 15 |
| 2 | UQ | 10 | 13 |
| 3 | Mediana | 7 | 10 |
| 4 | LQ | 6 | 9 |
| 5 | Min | 5 | 6 |
Rozwiązanie:
Rozważ poniższy diagram:
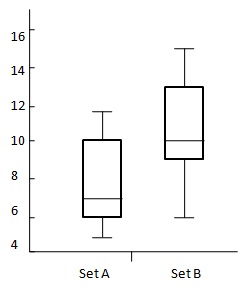
$ {OVS = 13 - 6 \\ [7pt] \ = 7 \\ [7pt] \ DBM = 10-3 \\ [7pt] \ = 4} $
Zastosuj formułę
$ {P = \ frac {DBM} {OVS} \ times 100 \\ [7pt] \ = \ frac {4} {7} \ times 100 \\ [7pt] \ = 57,14} $
Ponieważ wartość procentowa przekracza 33%, istnieje różnica między zestawem A a zestawem B. Jest prawdopodobne, że zestaw B jest większy niż zestaw A.