Statystyki - rozkład chi-kwadrat
Rozkład chi-kwadrat (chi-kwadrat lub rozkład $ {X ^ 2} $ -) ze stopniami swobody, k jest rozkładem sumy kwadratów k niezależnych standardowych normalnych zmiennych losowych. Jest to jeden z najczęściej używanych rozkładów prawdopodobieństwa w statystyce. Jest to szczególny przypadek rozkładu gamma.
Rozkład chi-kwadrat jest szeroko stosowany przez statystyków do obliczania:
Szacowanie przedziału ufności dla odchylenia standardowego populacji rozkładu normalnego przy użyciu odchylenia standardowego próby.
Sprawdzenie niezależności dwóch kryteriów klasyfikacji wielu zmiennych jakościowych.
Aby sprawdzić relacje między zmiennymi kategorialnymi.
Zbadanie wariancji próby, w której podstawowy rozkład jest normalny.
Testowanie odchyleń różnic między częstotliwościami oczekiwanymi i obserwowanymi.
Przeprowadzenie testu chi-kwadrat (test zgodności).
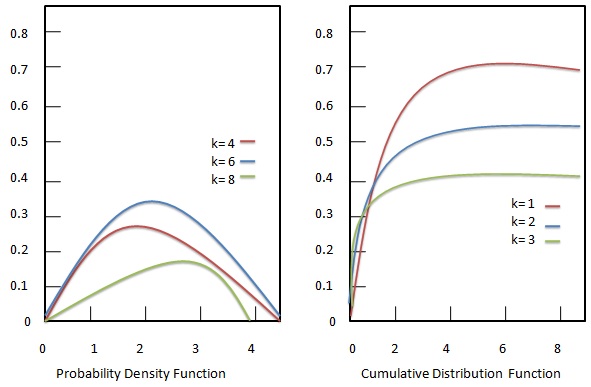
Funkcja gęstości prawdopodobieństwa
Funkcja gęstości prawdopodobieństwa rozkładu Chi-kwadrat jest podana jako:
Formuła
Gdzie -
$ {\ Gamma (\ frac {k} {2})} $ = Funkcja gamma mająca wartości w postaci zamkniętej dla parametru k.
$ {x} $ = zmienna losowa.
$ {k} $ = parametr liczby całkowitej.
Dystrybuanta
Dystrybucja skumulowana rozkładu Chi-kwadrat jest podana jako:
Formuła
Gdzie -
$ {\ gamma (s, t)} $ = niższa niepełna funkcja gamma.
$ {P (s, t)} $ = uregulowana funkcja gamma.
$ {x} $ = zmienna losowa.
$ {k} $ = parametr liczby całkowitej.