Xử lý tín hiệu kỹ thuật số - Tín hiệu DT cơ bản
Chúng ta đã thấy rằng các tín hiệu cơ bản có thể được biểu diễn như thế nào trong Miền thời gian liên tục. Hãy để chúng tôi xem các tín hiệu cơ bản có thể được biểu diễn như thế nào trong Miền thời gian rời rạc.
Trình tự xung đơn vị
Nó được ký hiệu là δ (n) trong miền thời gian rời rạc và có thể được định nghĩa là;
$$ \ delta (n) = \ begin {case} 1 và cho \ quad n = 0 \\ 0, & Nếu không thì \ end {case} $$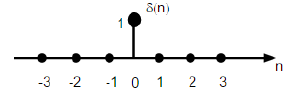
Tín hiệu bước đơn vị
Tín hiệu bước đơn vị thời gian rời rạc được định nghĩa là;
$$ U (n) = \ begin {case} 1, & cho \ quad n \ geq0 \\ 0 và cho \ quad n <0 \ end {case} $$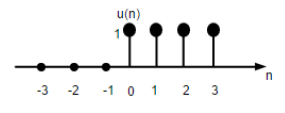
Hình trên cho thấy biểu diễn đồ họa của một hàm bước rời rạc.
Chức năng Đơn vị Ramp
Một hàm dốc đơn vị rời rạc có thể được định nghĩa là -
$$ r (n) = \ begin {case} n và cho \ quad n \ geq0 \\ 0 và cho \ quad n <0 \ end {case} $$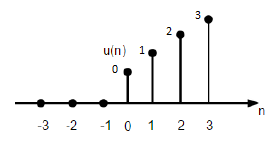
Hình trên cho thấy biểu diễn đồ họa của tín hiệu dốc rời rạc.
Hàm Parabol
Hàm parabol đơn vị rời rạc được ký hiệu là p (n) và có thể được định nghĩa là;
$$ p (n) = \ begin {case} \ frac {n ^ {2}} {2} và cho \ quad n \ geq0 \\ 0 và cho \ quad n <0 \ end {case} $$Về chức năng bước đơn vị, nó có thể được viết là;
$$ P (n) = \ frac {n ^ {2}} {2} U (n) $$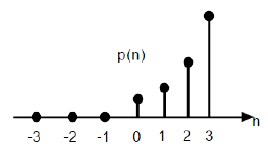
Hình trên cho thấy biểu diễn đồ họa của một dãy parabol.
Tín hiệu hình sin
Tất cả các tín hiệu thời gian liên tục là định kỳ. Các chuỗi hình sin thời gian rời rạc có thể có hoặc không tuần hoàn. Chúng phụ thuộc vào giá trị của ω. Để tín hiệu thời gian rời rạc có tính tuần hoàn thì tần số góc ω phải là bội số hữu tỉ của 2π.
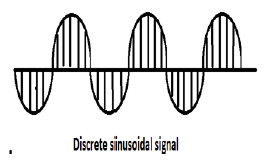
Một tín hiệu hình sin rời rạc được thể hiện trong hình trên.
Dạng rời rạc của tín hiệu hình sin có thể được biểu diễn ở định dạng -
$$ x (n) = A \ sin (\ omega n + \ phi) $$Ở đây A, ω và φ có nghĩa thông thường và n là số nguyên. Khoảng thời gian của tín hiệu hình sin rời rạc được cho bởi:
$$ N = \ frac {2 \ pi m} {\ omega} $$Trong đó, N và m là các số nguyên.