DSP - Các tín hiệu khác
Có những tín hiệu khác, là kết quả của hoạt động được thực hiện trên chúng. Một số loại tín hiệu phổ biến được thảo luận dưới đây.
Tín hiệu kết hợp
Tín hiệu thỏa mãn điều kiện $ x (t) = x * (- t) $ được gọi là tín hiệu liên hợp.
Cho $ x (t) = a (t) + jb (t) $ ... eqn. 1
Vì vậy, $ x (-t) = a (-t) + jb (-t) $
Và $ x * (- t) = a (-t) -jb (-t) $ ... eqn. 2
Theo điều kiện, $ x (t) = x * (- t) $
Nếu chúng ta so sánh cả hai phương trình dẫn xuất 1 và 2, chúng ta có thể thấy rằng phần thực là chẵn, trong khi phần ảo là lẻ. Đây là điều kiện để một tín hiệu có dạng liên hợp.
Kết hợp các tín hiệu chống đối xứng
Tín hiệu thỏa mãn điều kiện $ x (t) = -x * (- t) $ được gọi là tín hiệu phản đối xứng liên hợp
Cho $ x (t) = a (t) + jb (t) $ ... eqn. 1
Vậy $ x (-t) = a (-t) + jb (-t) $
Và $ x * (- t) = a (-t) -jb (-t) $
$ -x * (- t) = -a (-t) + jb (-t) $ ... eqn. 2
Theo điều kiện $ x (t) = -x * (- t) $
Bây giờ, một lần nữa so sánh, cả hai phương trình giống như chúng ta đã làm đối với tín hiệu liên hợp. Ở đây, chúng ta sẽ thấy rằng phần thực là số lẻ và phần ảo là số chẵn. Đây là điều kiện để một tín hiệu trở thành loại phản đối xứng liên hợp.
Thí dụ
Cho tín hiệu đã cho là $ x (t) = \ sin t + jt ^ {2} $.
Ở đây, phần thực $ \ sin t $ là số lẻ và phần ảo là $ t ^ 2 $ là số chẵn. Vì vậy, tín hiệu này có thể được phân loại là tín hiệu phản đối xứng liên hợp.
Bất kỳ chức năng nào cũng có thể được chia thành hai phần. Một phần là đối xứng liên hợp và một phần khác là phản đối xứng liên hợp. Vì vậy, bất kỳ tín hiệu x (t) nào có thể được viết dưới dạng
$$ x (t) = xcs (t) + xcas (t) $$Trong đó $ xcs (t) $ là tín hiệu đối xứng liên hợp và $ xcas (t) $ là tín hiệu phản đối xứng liên hợp
$$ xcs (t) = \ frac {[x (t) + x * (- t)]} {2} $$Và
$$ xcas (t) = \ frac {[x (t) -x * (- t)]} {2} $$Tín hiệu đối xứng nửa sóng
Khi một tín hiệu thỏa mãn điều kiện $ cx (t) = -x (t \ pm (\ frac {T_ {0}} {2})) $, nó được gọi là tín hiệu đối xứng nửa sóng. Ở đây, sự đảo ngược biên độ và dịch chuyển thời gian của tín hiệu diễn ra trong một nửa thời gian. Đối với tín hiệu đối xứng nửa sóng, giá trị trung bình sẽ bằng 0 nhưng đây không phải là trường hợp đảo ngược tình huống.
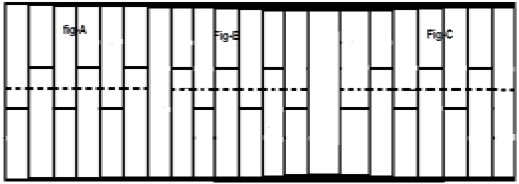
Xét một tín hiệu x (t) như trong hình A ở trên. Bước đầu tiên là thay đổi thời gian tín hiệu và đặt nó thành $ x [t - (\ frac {T} {2})] $. Vì vậy, tín hiệu mới được thay đổi như trong hình B. Tiếp theo, chúng tôi đảo ngược biên độ của tín hiệu, tức là làm cho nó $ -x [t - (\ frac {T} {2})] $ như trong hình C. Vì tín hiệu này tự lặp lại sau khi dịch chuyển nửa thời gian và đảo ngược biên độ, nó là tín hiệu đối xứng nửa sóng.
Tín hiệu trực giao
Hai tín hiệu x (t) và y (t) được cho là trực giao nếu chúng thỏa mãn hai điều kiện sau.
Condition 1 - $ \ int _ {- \ infty} ^ {\ infty} x (t) y (t) = 0 $ [cho tín hiệu không tuần hoàn]
Condition 2 - $ \ int x (t) y (t) = 0 $ [Đối với Tín hiệu tuần hoàn]
Các tín hiệu, chứa các sóng hài lẻ ( thứ 3 , thứ 5 , thứ 7 ...) và có tần số khác nhau, trực giao lẫn nhau với nhau.
Trong các tín hiệu loại lượng giác, hàm sin và hàm cosin cũng trực giao với nhau; miễn là chúng có cùng tần số và cùng pha. Theo cách tương tự, tín hiệu DC (Tín hiệu dòng điện một chiều) và tín hiệu hình sin cũng trực giao với nhau. Nếu x (t) và y (t) là hai tín hiệu trực giao và $ z (t) = x (t) + y (t) $ thì lũy thừa và năng lượng của z (t) có thể được viết là;
$$ P (z) = p (x) + p (y) $$ $$ E (z) = E (x) + E (y) $$Thí dụ
Phân tích tín hiệu: $ z (t) = 3 + 4 \ sin (2 \ pi t + 30 ^ 0) $
Ở đây, tín hiệu bao gồm một tín hiệu DC (3) và một hàm sin. Vì vậy, theo đặc tính của tín hiệu này là một tín hiệu trực giao và hai tín hiệu con trong nó là trực giao lẫn nhau.