DSP - Hoạt động trên sự dịch chuyển tín hiệu
Dịch chuyển có nghĩa là chuyển động của tín hiệu, trong miền thời gian (quanh trục Y) hoặc trong miền biên độ (quanh trục X). Theo đó, chúng ta có thể phân loại sự dịch chuyển thành hai loại có tên là Dịch chuyển thời gian và Dịch chuyển biên độ, chúng sẽ được thảo luận dưới đây.
Dịch chuyển thời gian
Dịch chuyển thời gian có nghĩa là, sự dịch chuyển của tín hiệu trong miền thời gian. Về mặt toán học, nó có thể được viết là
$$ x (t) \ rightarrow y (t + k) $$Giá trị K này có thể là dương hoặc có thể là âm. Theo dấu của giá trị k, chúng ta có hai loại chuyển dịch được đặt tên là Chuyển phải và Chuyển trái.
Trường hợp 1 (K> 0)
Khi K lớn hơn 0, sự dịch chuyển của tín hiệu diễn ra về phía "trái" trong miền thời gian. Do đó, loại dịch chuyển này được gọi là dịch chuyển trái của tín hiệu.
Example
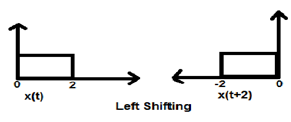
Trường hợp 2 (K <0)
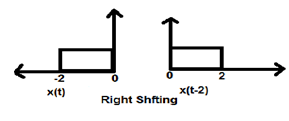
Khi K nhỏ hơn 0, sự dịch chuyển của tín hiệu diễn ra theo hướng sang phải trong miền thời gian. Do đó, kiểu chuyển dịch này được gọi là Chuyển dịch phải.
Example
Hình dưới đây cho thấy sự dịch chuyển sang phải của một tín hiệu bằng 2.
Biên độ dịch chuyển
Dịch chuyển biên độ có nghĩa là sự dịch chuyển của tín hiệu trong miền biên độ (quanh trục X). Về mặt toán học, nó có thể được biểu diễn dưới dạng:
$$ x (t) \ rightarrow x (t) + K $$Giá trị K này có thể dương hoặc âm. Theo đó, chúng ta có hai loại dịch chuyển biên độ sẽ được thảo luận dưới đây.
Trường hợp 1 (K> 0)
Khi K lớn hơn 0, sự dịch chuyển của tín hiệu diễn ra theo hướng lên trên trục x. Do đó, kiểu chuyển dịch này được gọi là chuyển dịch hướng lên.
Example
Chúng ta hãy xem xét một tín hiệu x (t) được cho là;
$$ x = \ begin {case} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {case} $$Chúng ta đã lấy K = + 1 để tín hiệu mới có thể được viết là -
$ y (t) \ rightarrow x (t) + 1 $ Vì vậy, cuối cùng y (t) có thể được viết thành;
$$ x (t) = \ begin {case} 1, & t <0 \\ 2, & 0 \ leq t \ leq 2 \\ 1, & t> 0 \ end {case} $$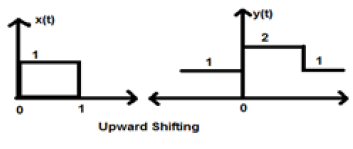
Trường hợp 2 (K <0)
Khi K nhỏ hơn 0, sự dịch chuyển của tín hiệu diễn ra theo hướng đi xuống trong trục X. Do đó, nó được gọi là sự dịch chuyển xuống của tín hiệu.
Example
Chúng ta hãy xem xét một tín hiệu x (t) được cho là;
$$ x (t) = \ begin {case} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {case} $$Chúng ta đã lấy K = -1 để tín hiệu mới có thể được viết là;
$ y (t) \ rightarrow x (t) -1 $ Vì vậy, cuối cùng y (t) có thể được viết thành;
$$ y (t) = \ begin {case} -1, & t <0 \\ 0, & 0 \ leq t \ leq 2 \\ -1, & t> 0 \ end {case} $$