Xử lý tín hiệu kỹ thuật số - Tín hiệu-Định nghĩa

Định nghĩa

Bất cứ thứ gì mang thông tin đều có thể được gọi là tín hiệu. Nó cũng có thể được định nghĩa là một đại lượng vật lý thay đổi theo thời gian, nhiệt độ, áp suất hoặc với bất kỳ biến độc lập nào như tín hiệu giọng nói hoặc tín hiệu video.

Quá trình hoạt động trong đó các đặc tính của tín hiệu (Biên độ, hình dạng, pha, tần số, v.v.) trải qua một sự thay đổi được gọi là quá trình xử lý tín hiệu.

Note- Bất kỳ tín hiệu không mong muốn nào can thiệp vào tín hiệu chính được gọi là nhiễu. Vì vậy, nhiễu cũng là một tín hiệu nhưng không mong muốn.

Theo cách biểu diễn và xử lý của chúng, các tín hiệu có thể được phân loại thành nhiều loại khác nhau, chi tiết sẽ được thảo luận dưới đây.

Tín hiệu thời gian liên tục

Tín hiệu thời gian liên tục được xác định dọc theo một chu kỳ thời gian và do đó, được biểu diễn bằng một biến độc lập liên tục. Tín hiệu thời gian liên tục thường được gọi là tín hiệu tương tự.

Loại tín hiệu này thể hiện tính liên tục cả về biên độ và thời gian. Chúng sẽ có giá trị tại mỗi thời điểm. Các hàm sin và côsin là ví dụ tốt nhất về Tín hiệu thời gian liên tục.

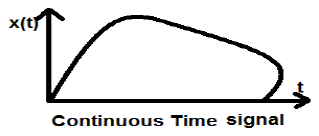
Tín hiệu được hiển thị ở trên là một ví dụ về tín hiệu thời gian liên tục vì chúng ta có thể nhận được giá trị của tín hiệu tại mỗi thời điểm của thời gian.

Tín hiệu thời gian rời rạc

Các tín hiệu, được xác định tại các thời điểm rời rạc được gọi là tín hiệu rời rạc. Do đó, mọi biến độc lập đều có giá trị khác biệt. Do đó, chúng được biểu diễn dưới dạng một dãy số.

Mặc dù tín hiệu giọng nói và video có đặc quyền được biểu diễn ở cả định dạng thời gian liên tục và rời rạc; trong những trường hợp nhất định, chúng giống hệt nhau. Biên độ cũng cho thấy các đặc tính rời rạc. Ví dụ hoàn hảo về điều này là một tín hiệu kỹ thuật số; mà cả hai biên độ và thời gian đều rời rạc.

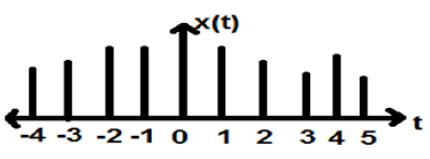
Hình trên mô tả đặc tính biên độ rời rạc của một tín hiệu rời rạc trong một khoảng thời gian. Về mặt toán học, các loại tín hiệu này có thể được công thức hóa thành;

$$ x = \ left \ {x \ left [n \ right] \ right \}, \ quad - \ infty <n <\ infty $$

Trong đó, n là một số nguyên.

Nó là một dãy số x, trong đó số ^thứ n trong dãy được biểu diễn là x [n].