DSP - Hoạt động trên quy mô tín hiệu
Tỷ lệ của một tín hiệu có nghĩa là, một hằng số được nhân với thời gian hoặc biên độ của tín hiệu.
Tỷ lệ thời gian
Nếu một hằng số được nhân với trục thời gian thì nó được gọi là Tỷ lệ thời gian. Điều này có thể được biểu diễn bằng toán học là;
$ x (t) \ rightarrow y (t) = x (\ alpha t) $ hoặc $ x (\ frac {t} {\ alpha}) $; trong đó α ≠ 0
Vì vậy, trục y giống nhau, độ lớn trục x giảm hoặc tăng theo dấu của hằng số (cho dù dương hay âm). Do đó, tỷ lệ cũng có thể được chia thành hai loại như được thảo luận dưới đây.
Nén thời gian
Bất cứ khi nào alpha lớn hơn 0, biên độ của tín hiệu được chia cho alpha trong khi giá trị của trục Y vẫn giữ nguyên. Điều này được gọi là Nén thời gian.
Example
Chúng ta hãy xem xét một tín hiệu x (t), được hiển thị như trong hình dưới đây. Chúng ta hãy lấy giá trị của alpha là 2. Vì vậy, y (t) sẽ là x (2t), được minh họa trong hình bên.

Rõ ràng, chúng ta có thể thấy từ các hình trên rằng độ lớn thời gian theo trục y không đổi nhưng biên độ theo trục x giảm từ 4 xuống 2. Do đó, nó là trường hợp Nén thời gian.
Mở rộng thời gian
Khi thời gian được chia cho hằng số alpha, cường độ trục Y của tín hiệu được nhân với alpha lần, giữ nguyên độ lớn trục X. Do đó, đây được gọi là tín hiệu kiểu mở rộng thời gian.
Example
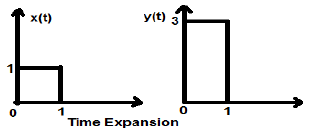
Chúng ta hãy xem xét một tín hiệu bình phương x (t), độ lớn 1. Khi chúng ta chia tỷ lệ thời gian của nó theo một hằng số 3, sao cho $ x (t) \ rightarrow y (t) \ rightarrow x (\ frac {t} {3} ) $, sau đó biên độ của tín hiệu được sửa đổi 3 lần được thể hiện trong hình bên dưới.
Tỷ lệ biên độ
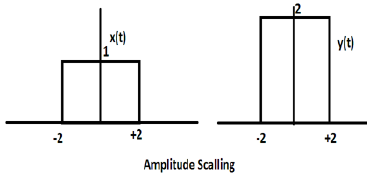
Nhân của một hằng số với biên độ của tín hiệu gây ra tỷ lệ biên độ. Tùy thuộc vào dấu hiệu của hằng số, nó có thể là tỷ lệ biên độ hoặc sự suy giảm. Chúng ta hãy xem xét một tín hiệu sóng vuông x (t) = Π (t / 4).
Giả sử chúng ta định nghĩa một hàm khác y (t) = 2 Π (t / 4). Trong trường hợp này, giá trị của trục y sẽ được nhân đôi, giữ nguyên giá trị trục thời gian. Được minh họa trong hình bên dưới.
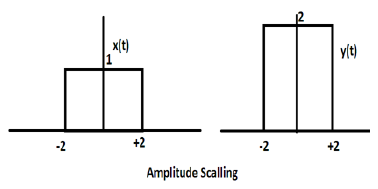
Xét một hàm sóng vuông khác được định nghĩa là z (t) trong đó z (t) = 0,5 Π (t / 4). Ở đây, biên độ của hàm z (t) sẽ bằng một nửa của x (t) tức là trục thời gian được giữ nguyên, trục biên độ sẽ giảm đi một nửa. Điều này được minh họa bằng hình dưới đây.