DSP - Tính toán tại chỗ
Việc sử dụng bộ nhớ hiệu quả này rất quan trọng đối với việc thiết kế phần cứng nhanh để tính toán FFT. Thuật ngữ tính toán tại chỗ được sử dụng để mô tả việc sử dụng bộ nhớ này.
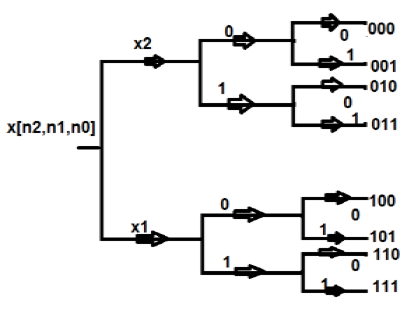
Phân rã theo trình tự thời gian
Trong cấu trúc này, chúng tôi biểu diễn tất cả các điểm ở định dạng nhị phân, tức là ở 0 và 1. Sau đó, chúng tôi đảo ngược các cấu trúc đó. Chuỗi mà chúng ta nhận được sau đó được gọi là chuỗi đảo ngược bit. Đây còn được gọi là số thập phân trong chuỗi thời gian. Tính toán tại chỗ của DFT tám điểm được hiển thị ở định dạng bảng như hình dưới đây:
| ĐIỂM | ĐỊNH DẠNG BINARY | REVERSAL | ĐIỂM TƯƠNG ĐƯƠNG |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
Phân rã theo chuỗi tần số
Ngoài chuỗi thời gian, chuỗi điểm N cũng có thể được biểu diễn theo tần số. Chúng ta hãy xem một chuỗi bốn điểm để hiểu rõ hơn.
Cho dãy là $ x [0], x [1], x [2], x [3], x [4], x [5], x [6], x [7] $. Ban đầu, chúng tôi sẽ nhóm hai điểm thành một nhóm. Về mặt toán học, chuỗi này có thể được viết là;
$$ x [k] = \ sum_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$Bây giờ chúng ta hãy tạo một nhóm của dãy số 0 đến 3 và một nhóm khác của dãy số 4 đến 7. Bây giờ, về mặt toán học, điều này có thể được thể hiện như;
$$ \ displaystyle \ sum \ limit_ {n = 0} ^ {\ frac {N} {2} -1} x [n] W_N ^ {nk} + \ displaystyle \ sum \ limit_ {n = N / 2} ^ {N-1} x [n] W_N ^ {nk} $$Chúng ta hãy thay n bởi r, trong đó r = 0, 1, 2…. (N / 2-1). Về mặt toán học,
$$ \ displaystyle \ sum \ limit_ {n = 0} ^ {\ frac {N} {2} -1} x [r] W_ {N / 2} ^ {nr} $$Ban đầu chúng tôi lấy bốn điểm đầu tiên (x [0], x [1], x [2], x [3]) và cố gắng biểu diễn chúng theo phương pháp toán học như sau:
$ \ sum_ {n = 0} ^ 3x [n] W_8 ^ {nk} + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(n + 4) k} $
$ = \ lbrace \ sum_ {n = 0} ^ 3x [n] + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(4) k} \ rbrace \ times W_8 ^ {nk} $
bây giờ $ X [0] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) $
$ X [1] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) W_8 ^ {nk} $
$ = [X [0] -X [4] + (X [1] -X [5]) W_8 ^ 1 + (X [2] -X [6]) W_8 ^ 2 + (X [3] -X [7]) W_8 ^ 3 $
Chúng ta có thể chia nó thành hai phần nữa, có nghĩa là thay vì chia chúng thành chuỗi 4 điểm, chúng ta có thể chia chúng thành chuỗi 2 điểm.