DSP - Hệ thống bất biến thời gian
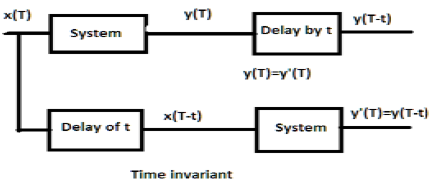
Đối với một hệ thống bất biến thời gian, đầu ra và đầu vào phải bị trễ một đơn vị thời gian nào đó. Bất kỳ độ trễ nào được cung cấp trong đầu vào phải được phản ánh trong đầu ra đối với một hệ thống bất biến theo thời gian.
Ví dụ
a) $y(T) = x(2T)$
Nếu biểu thức trên, trước tiên nó được chuyển qua hệ thống và sau đó qua thời gian trễ (như thể hiện trong phần trên của hình); thì đầu ra sẽ trở thành $ x (2T-2t) $. Bây giờ, biểu thức tương tự được chuyển qua một khoảng thời gian trễ trước rồi sau đó qua hệ thống (như thể hiện trong phần dưới của hình). Đầu ra sẽ trở thành $ x (2T-t) $.
Do đó, hệ thống không phải là một hệ thống bất biến theo thời gian.
b) $y(T) = \sin [x(T)]$
Nếu tín hiệu đầu tiên được truyền qua hệ thống và sau đó qua quá trình trễ thời gian, đầu ra là $ \ sin x (Tt) $. Tương tự, nếu hệ thống được chuyển qua khoảng thời gian trễ trước rồi đến hệ thống thì đầu ra sẽ là $ \ sin x (Tt) $. Chúng ta có thể thấy rõ rằng cả hai đầu ra đều giống nhau. Do đó, hệ thống là bất biến theo thời gian.