DSP - Phân loại tín hiệu CT
Các tín hiệu thời gian liên tục có thể được phân loại theo các điều kiện hoặc hoạt động khác nhau được thực hiện trên các tín hiệu.
Tín hiệu chẵn và lẻ
Tín hiệu đồng đều
Một tín hiệu được cho là ngay cả khi nó thỏa mãn điều kiện sau;
$$ x (-t) = x (t) $$Sự đảo ngược thời gian của tín hiệu không ngụ ý bất kỳ sự thay đổi nào về biên độ ở đây. Ví dụ, hãy xem xét sóng tam giác được hiển thị bên dưới.
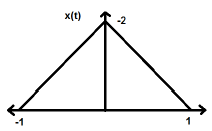
Tín hiệu tam giác là tín hiệu chẵn. Vì, nó đối xứng về trục Y. Có thể nói đó là hình ảnh phản chiếu về trục Y.
Hãy xem xét một tín hiệu khác như trong hình bên dưới.
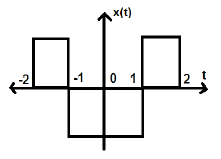
Chúng ta có thể thấy rằng tín hiệu trên là đồng đều vì nó đối xứng qua trục Y.
Tín hiệu kỳ lạ
Một tín hiệu được cho là kỳ lạ, nếu nó thỏa mãn điều kiện sau
$$ x (-t) = -x (t) $$Ở đây, cả sự đảo ngược thời gian và sự thay đổi biên độ diễn ra đồng thời.
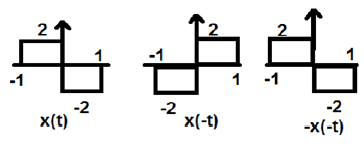
Trong hình trên, chúng ta có thể thấy một tín hiệu bước x (t). Để kiểm tra xem đó có phải là tín hiệu lẻ hay không, đầu tiên chúng ta thực hiện đảo ngược thời gian tức là x (-t) và kết quả như hình bên. Sau đó, chúng tôi đảo ngược biên độ của tín hiệu kết quả tức là –x (-t) và chúng tôi nhận được kết quả như trong hình.
Nếu chúng ta so sánh dạng sóng thứ nhất và thứ ba, chúng ta có thể thấy rằng chúng giống nhau, tức là x (t) = -x (-t), thỏa mãn tiêu chí của chúng ta. Do đó, tín hiệu trên là tín hiệu Lẻ.
Một số kết quả quan trọng liên quan đến tín hiệu chẵn và lẻ được đưa ra dưới đây.
- Even × Even = Even
- Odd × Odd = Chẵn
- Chẵn × Lẻ = Lẻ
- Even ± Even = Even
- Odd ± Odd = Lẻ
- Chẵn ± Lẻ = Không chẵn cũng không lẻ
Biểu diễn bất kỳ tín hiệu nào thành dạng chẵn hoặc lẻ
Một số tín hiệu không thể được phân loại trực tiếp thành loại chẵn hoặc lẻ. Chúng được biểu diễn dưới dạng sự kết hợp của cả tín hiệu chẵn và lẻ.
$$ x (t) \ rightarrow x_ {e} (t) + x_ {0} (t) $$Trong đó x e (t) đại diện cho tín hiệu chẵn và x o (t) đại diện cho tín hiệu lẻ
$$ x_ {e} (t) = \ frac {[x (t) + x (-t)]} {2} $$Và
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$Thí dụ
Tìm phần chẵn và lẻ của tín hiệu $ x (n) = t + t ^ {2} + t ^ {3} $
Solution - Từ đảo ngược x (n), ta được
$$ x (-n) = -t + t ^ {2} -t ^ {3} $$
Bây giờ, theo công thức, phần chẵn
$$ x_ {e} (t) = \ frac {x (t) + x (-t)} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) + (- t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t ^ {2} $$
Tương tự, theo công thức, phần lẻ là
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) - (- t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t + t ^ {3} $$
Tín hiệu định kỳ và không định kỳ
Tín hiệu định kỳ
Tín hiệu định kỳ tự lặp lại sau một khoảng thời gian nhất định. Chúng ta có thể hiển thị điều này ở dạng phương trình như sau:
$$ x (t) = x (t) \ pm nT $$Trong đó, n = một số nguyên (1,2,3 ……)
T = Khoảng thời gian cơ bản (FTP) ≠ 0 và ≠ ∞
Khoảng thời gian cơ bản (FTP) là giá trị dương và cố định nhỏ nhất của thời gian mà tín hiệu là định kỳ.
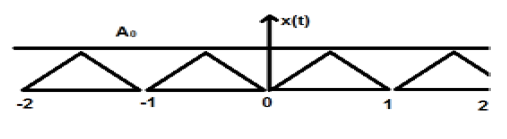
Một tín hiệu hình tam giác được thể hiện trong hình trên với biên độ A. Ở đây, tín hiệu được lặp lại sau mỗi 1 giây. Do đó, chúng ta có thể nói rằng tín hiệu là định kỳ và FTP của nó là 1 giây.
Tín hiệu không định kỳ
Đơn giản, chúng ta có thể nói, các tín hiệu không tuần hoàn về bản chất là không tuần hoàn. Rõ ràng, những tín hiệu này sẽ không lặp lại sau bất kỳ khoảng thời gian nào.
Các tín hiệu không tuần hoàn không theo một định dạng nhất định; do đó, không có phương trình toán học cụ thể nào có thể mô tả chúng.
Tín hiệu năng lượng và công suất
Một tín hiệu được cho là tín hiệu Năng lượng, nếu và chỉ khi, tổng năng lượng chứa là hữu hạn và khác không (0 <E <∞). Do đó, đối với bất kỳ tín hiệu dạng năng lượng nào, tổng tín hiệu chuẩn hóa là hữu hạn và khác không.
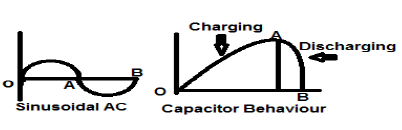
Tín hiệu dòng điện xoay chiều hình sin là một ví dụ hoàn hảo về tín hiệu loại Năng lượng vì nó ở nửa chu kỳ dương trong một trường hợp và sau đó là âm trong nửa chu kỳ tiếp theo. Do đó, công suất trung bình của nó trở thành không.
Tụ điện không mất mát cũng là một ví dụ hoàn hảo về tín hiệu kiểu Năng lượng vì khi nó được kết nối với nguồn, nó sẽ sạc đến mức tối ưu và khi nguồn được tháo ra, nó sẽ tiêu tán lượng năng lượng tương đương đó qua một tải và làm cho công suất trung bình của nó số không.
Đối với bất kỳ tín hiệu hữu hạn nào x (t), năng lượng có thể được ký hiệu là E và được viết là;
$$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$Mật độ phổ của tín hiệu dạng năng lượng cho biết lượng năng lượng được phân bố ở các mức tần số khác nhau.
Tín hiệu loại nguồn
Một tín hiệu được cho là tín hiệu loại công suất, nếu và chỉ khi, công suất trung bình chuẩn hóa là hữu hạn và khác 0 tức là (0 <p <∞). Đối với tín hiệu loại công suất, công suất trung bình chuẩn hóa là hữu hạn và khác không. Hầu hết tất cả các tín hiệu tuần hoàn là tín hiệu công suất và công suất trung bình của chúng là hữu hạn và khác không.
Ở dạng toán học, lũy thừa của tín hiệu x (t) có thể được viết dưới dạng;
$$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$Sự khác biệt giữa tín hiệu năng lượng và công suất
Bảng sau đây tóm tắt sự khác biệt của Tín hiệu Năng lượng và Công suất.
| Tín hiệu nguồn | Tín hiệu năng lượng |
|---|---|
| Tín hiệu tuần hoàn thực tế là tín hiệu công suất. | Tín hiệu không tuần hoàn là tín hiệu năng lượng. |
| Ở đây, công suất trung bình chuẩn hóa là hữu hạn và khác không. | Ở đây, tổng năng lượng chuẩn hóa là hữu hạn và khác không. |
|
Về mặt toán học, $$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$ |
Về mặt toán học, $$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$ |
| Sự tồn tại của những tín hiệu này là vô hạn theo thời gian. | Những tín hiệu này tồn tại trong một khoảng thời gian giới hạn. |
| Năng lượng của tín hiệu điện là vô hạn trong thời gian vô hạn. | Công suất của tín hiệu năng lượng bằng 0 trong thời gian vô hạn. |
Các ví dụ đã giải quyết
Example 1 - Tìm Công suất của tín hiệu $ z (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) + 4 \ sin (3 \ Pi + 30 ^ {o}) $
Solution- Hai tín hiệu trên trực giao với nhau vì các số hạng tần số của chúng giống nhau và chúng có cùng độ lệch pha. Vì vậy, tổng sức mạnh sẽ là tổng của các quyền lực riêng lẻ.
Cho $ z (t) = x (t) + y (t) $
Trong đó $ x (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) $ và $ y (t) = 4 \ sin (3 \ Pi + 30 ^ {o}) $
Lũy thừa của $ x (t) = \ frac {2 ^ {2}} {2} = 2 $
Lũy thừa của $ y (t) = \ frac {4 ^ {2}} {2} = 8 $
Do đó, $ P (z) = p (x) + p (y) = 2 + 8 = 10 $ … Trả lời.
Example 2 - Kiểm tra xem tín hiệu đã cho $ x (t) = t ^ {2} + j \ sin t $ có liên hợp hay không?
Solution- Ở đây, phần thực của t 2 là phần chẵn và phần lẻ (ảo) là $ \ sin t $ là phần lẻ. Vậy tín hiệu trên là tín hiệu Conjugate.
Example 3 - Xác minh xem $ X (t) = \ sin \ omega t $ là tín hiệu lẻ hay tín hiệu chẵn.
Solution - Cho $ X (t) = \ sin \ omega t $
Khi đảo ngược thời gian, chúng ta sẽ nhận được $ \ sin (- \ omega t) $
Nhưng chúng ta biết rằng $ \ sin (- \ phi) = - \ sin \ phi $.
Vì thế,
$$ \ sin (- \ omega t) = - \ sin \ omega t $$Điều này thỏa mãn điều kiện cho một tín hiệu là số lẻ. Do đó, $ \ sin \ omega t $ là một tín hiệu kỳ lạ.