DSP - Biến đổi Fourier nhanh
Trong các phương pháp DFT trước đó, chúng ta đã thấy rằng phần tính toán quá dài. Chúng tôi muốn giảm điều đó. Điều này có thể được thực hiện thông qua FFT hoặc biến đổi Fourier nhanh. Vì vậy, chúng ta có thể nói FFT không là gì khác ngoài việc tính toán biến đổi Fourier rời rạc trong một định dạng thuật toán, trong đó phần tính toán sẽ được giảm bớt.
Ưu điểm chính của việc có FFT là thông qua nó, chúng ta có thể thiết kế các bộ lọc FIR. Về mặt toán học, FFT có thể được viết như sau;
$$ x [K] = \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$Hãy để chúng tôi lấy một ví dụ để hiểu nó tốt hơn. Chúng tôi đã xem xét tám điểm có tên từ $ x_0 \ quad đến \ quad x_7 $. Chúng tôi sẽ chọn các số hạng chẵn trong một nhóm và các số hạng lẻ trong nhóm kia. Chế độ xem sơ đồ của những điều nói trên đã được hiển thị bên dưới -
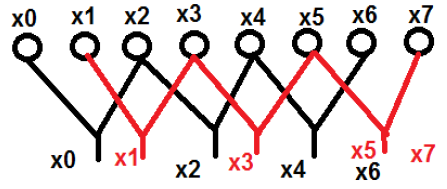
Ở đây, các điểm x 0 , x 2 , x 4 và x 6 đã được nhóm vào một loại và tương tự, các điểm x 1 , x 3 , x 5 và x 7 đã được đưa vào một loại khác. Bây giờ, chúng ta có thể thêm chúng thành một nhóm hai người và có thể tiến hành tính toán. Bây giờ, chúng ta hãy xem việc chia thành hai phần tiếp theo này giúp ích như thế nào trong việc tính toán.
$ x [k] = \ displaystyle \ sum \ limit_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_N ^ {2rk} + \ displaystyle \ sum \ limit_ {r = 0 } ^ {\ frac {N} {2} -1} x [2r + 1] W_N ^ {(2r + 1) k} $
$ = \ sum_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_ {N / 2} ^ {rk} + \ sum_ {r = 0} ^ {\ frac {N } {2} -1} x [2r + 1] W_ {N / 2} ^ {rk} \ times W_N ^ k $
$ = G [k] + H [k] \ lần W_N ^ k $
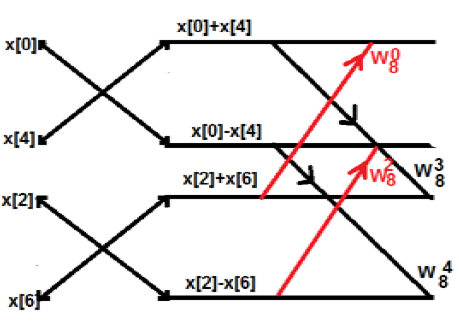
Ban đầu, chúng tôi lấy một dãy tám điểm, nhưng sau đó chúng tôi chia dãy đó thành hai phần G [k] và H [k]. G [k] là phần chẵn trong khi H [k] là phần lẻ. Nếu chúng ta muốn nhận ra nó thông qua một sơ đồ, thì nó có thể được hiển thị như dưới đây:
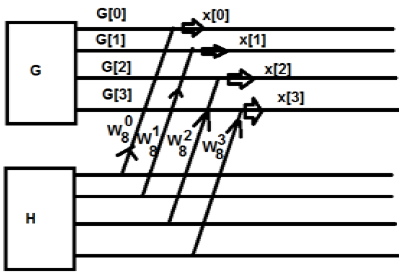
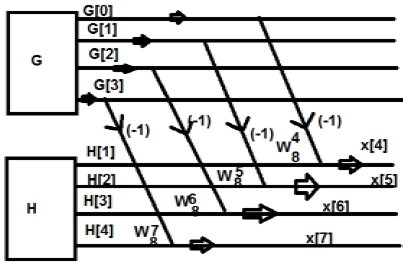
Từ hình trên, chúng ta có thể thấy rằng
$ W_8 ^ 4 = -1 $
$ W_8 ^ 5 = -W_8 ^ 1 $
$ W_8 ^ 6 = -W_8 ^ 2 $
$ W_8 ^ 7 = -W_8 ^ 3 $
Tương tự, các giá trị cuối cùng có thể được viết như sau:
$ G [0] -H [0] = x [4] $
$ G [1] -W_8 ^ 1H [1] = x [5] $
$ G [2] -W_8 ^ 2H [2] = x [6] $
$ G [1] -W_8 ^ 3H [3] = x [7] $
Trên đây là một chuỗi tuần hoàn. Nhược điểm của hệ thống này là K không thể bị phá vỡ quá 4 điểm. Bây giờ chúng ta hãy chia nhỏ những điều trên thành nhiều hơn nữa. Chúng ta sẽ nhận được những cấu trúc như thế này
Thí dụ
Xét dãy x [n] = {2,1, -1, -3,0,1,2,1}. Tính FFT.
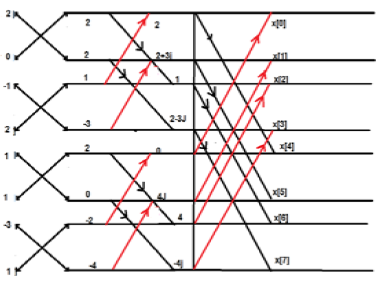
Solution - Dãy đã cho là x [n] = {2,1, -1, -3,0,1,2,1}
Sắp xếp các điều khoản như hình dưới đây;