Digitale Signalverarbeitung - Grundlegende CT-Signale

Zum Testen eines Systems werden im Allgemeinen Standard- oder Basissignale verwendet. Diese Signale sind die Grundbausteine ​​für viele komplexe Signale. Daher spielen sie eine sehr wichtige Rolle bei der Untersuchung von Signalen und Systemen.

Einheitsimpuls oder Delta-Funktion

Ein Signal, das die Bedingung $ \ delta (t) = \ lim _ {\ epsilon \ to \ infty} x (t) $ erfüllt, ist als Einheitsimpulssignal bekannt. Dieses Signal tendiert gegen unendlich, wenn t = 0 ist, und gegen Null, wenn t ≤ 0 ist, so dass die Fläche unter seiner Kurve immer gleich eins ist. Die Delta-Funktion hat überall bei t = 0 die Amplitude Null excunit_impulse.jpgept.

Eigenschaften des Einheitsimpulssignals

• δ (t) ist ein gerades Signal.
• δ (t) ist ein Beispiel für weder ein Energie- noch ein Leistungssignal (NENP).
• Der Bereich des Einheitsimpulssignals kann wie folgt geschrieben werden:
$$ A = \ int _ {- \ infty} ^ {\ infty} \ delta (t) dt = \ int _ {- \ infty} ^ {\ infty} \ lim _ {\ epsilon \ bis 0} x (t) dt = \ lim _ {\ epsilon \ to 0} \ int _ {- \ infty} ^ {\ infty} [x (t) dt] = 1 $$
• Gewicht oder Stärke des Signals können geschrieben werden als;
$$ y (t) = A \ delta (t) $$
• Der Bereich des gewichteten Impulssignals kann geschrieben werden als -
$$ y (t) = \ int _ {- \ infty} ^ {\ infty} y (t) dt = \ int _ {- \ infty} ^ {\ infty} A \ delta (t) = A [\ int _ {- \ infty} ^ {\ infty} \ delta (t) dt] = A = 1 = Wigthedimpulse $$

Einheitsschritt-Signal

Ein Signal, das die folgenden zwei Bedingungen erfüllt:

• $ U (t) = 1 (wenn \ quad t \ geq 0) und $
• $ U (t) = 0 (wenn \ quad t <0) $

ist als Einheitsschritt-Signal bekannt.

Es hat die Eigenschaft, eine Diskontinuität bei t = 0 anzuzeigen. Am Punkt der Diskontinuität ist der Signalwert durch den Durchschnitt des Signalwerts gegeben. Dieses Signal wurde kurz vor und nach dem Punkt der Diskontinuität aufgenommen (gemäß Gibbs Phänomenen).

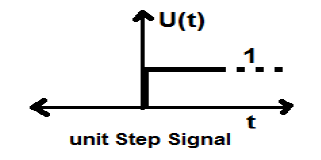
Wenn wir einem anderen zeitskalierten Stufensignal ein Schrittsignal hinzufügen, ist das Ergebnis Eins. Es ist ein Leistungssignal und der Leistungswert beträgt 0,5. Der Effektivwert (Root Mean Square) beträgt 0,707 und sein Durchschnittswert beträgt ebenfalls 0,5

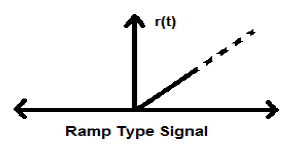
Rampensignal

Die Integration des Schrittsignals führt zu einem Rampensignal. Es wird durch r (t) dargestellt. Das Rampensignal erfüllt auch die Bedingung $ r (t) = \ int _ {- \ infty} ^ {t} U (t) dt = tU (t) $. Es handelt sich weder um ein Signal vom Typ Energie noch Leistung (NENP).

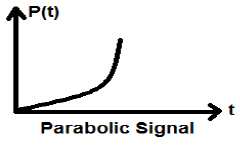
Parabolisches Signal

Die Integration des Rampensignals führt zu einem parabolischen Signal. Es wird durch p (t) dargestellt. Das parabolische Signal erfüllt auch die Bedingung $ p (t) = \ int _ {- \ infty} ^ {t} r (t) dt = (t ^ {2} / 2) U (t) $. Es handelt sich weder um ein Signal vom Typ Energie noch Leistung (NENP).

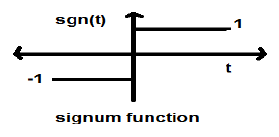
Signum-Funktion

Diese Funktion wird dargestellt als

$$ sgn (t) = \ begin {Fälle} 1 & für \ quad t> 0 \\ - 1 & für \ quad t <0 \ end {Fälle} $$

Es ist ein Leistungssignal. Der Leistungswert und der Effektivwert (Root Mean Square) sind beide 1. Der Durchschnittswert der Signumfunktion ist Null.

Sinc Funktion

Es ist auch eine Funktion des Sinus und wird geschrieben als -

$$ SinC (t) = \ frac {Sin \ Pi t} {\ Pi T} = Sa (\ Pi t) $$

Eigenschaften der Sinc-Funktion

• Es ist ein Energiesignal.

• $ Sinc (0) = \ lim_ {t \ bis 0} \ frac {\ sin \ Pi t} {\ Pi t} = 1 $

• $ Sinc (\ infty) = \ lim_ {t \ to \ infty} \ frac {\ sin \ Pi \ infty} {\ Pi \ infty} = 0 $ (Der Bereich von sinπ∞ variiert zwischen -1 bis +1, aber alles ist geteilt durch unendlich ist gleich Null)

• Wenn $ \ sin c (t) = 0 => \ sin \ Pi t = 0 $

  $ \ Rightarrow \ Pi t = n \ Pi $

  $ \ Rightarrow t = n (n \ neq 0) $

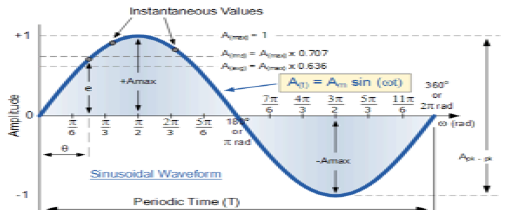
Sinussignal

Ein Signal, das von Natur aus kontinuierlich ist, wird als kontinuierliches Signal bezeichnet. Allgemeines Format eines sinusförmigen Signals ist

$$ x (t) = A \ sin (\ omega t + \ phi) $$

Hier,

A = Amplitude des Signals

ω = Winkelfrequenz des Signals (gemessen im Bogenmaß)

φ = Phasenwinkel des Signals (gemessen im Bogenmaß)

Die Tendenz dieses Signals besteht darin, sich nach einer bestimmten Zeitspanne zu wiederholen, was als periodisches Signal bezeichnet wird. Die Zeitdauer des Signals ist gegeben als;

$$ T = \ frac {2 \ pi} {\ omega} $$

Die schematische Ansicht des sinusförmigen Signals ist unten gezeigt.

Rechteckige Funktion

Ein Signal wird als rechteckiger Funktionstyp bezeichnet, wenn es die folgende Bedingung erfüllt:

$$ \ pi (\ frac {t} {\ tau}) = \ begin {Fällen} 1, & für \ quad t \ leq \ frac {\ tau} {2} \\ 0, & Andernfalls \ end {Fälle} $$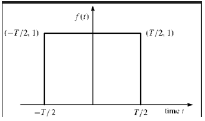

Da dieses Signal symmetrisch zur Y-Achse ist, wird es als gerades Signal bezeichnet.

Dreieckiges Impulssignal

Jedes Signal, das die folgende Bedingung erfüllt, wird als Dreieckssignal bezeichnet.

$$ \ Delta (\ frac {t} {\ tau}) = \ begin {case} 1 - (\ frac {2 | t |} {\ tau}) & für | t | <\ frac {\ tau} { 2} \\ 0 & für | t |> \ frac {\ tau} {2} \ end {case} $$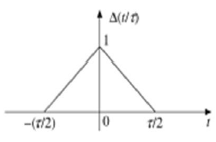

Dieses Signal ist symmetrisch zur Y-Achse. Daher wird es auch als gerades Signal bezeichnet.