DSP - Zeitinvariante Systeme

Bei einem zeitinvarianten System sollten Ausgabe und Eingabe um eine Zeiteinheit verzögert sein. Jede in der Eingabe vorgesehene Verzögerung muss für ein zeitinvariantes System in der Ausgabe berücksichtigt werden.

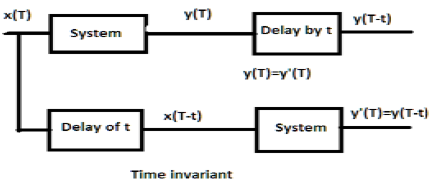
Beispiele

a) $y(T) = x(2T)$

Wenn der obige Ausdruck vorliegt, wird er zuerst durch das System und dann durch die Zeitverzögerung geleitet (wie im oberen Teil der Figur gezeigt); dann wird die Ausgabe zu $ ​​x (2T-2t) $. Nun wird der gleiche Ausdruck zuerst durch eine Zeitverzögerung und dann durch das System geleitet (wie im unteren Teil der Abbildung gezeigt). Die Ausgabe wird zu $ ​​x (2T-t) $.

Daher ist das System kein zeitinvariantes System.

b) $y(T) = \sin [x(T)]$

Wenn das Signal zuerst durch das System und dann durch den Zeitverzögerungsprozess geleitet wird, ist der Ausgang $ \ sin x (Tt) $. In ähnlicher Weise ist die Ausgabe $ \ sin x (Tt) $, wenn das System zuerst die Zeitverzögerung und dann das System durchläuft. Wir können deutlich sehen, dass beide Ausgänge gleich sind. Daher ist das System zeitinvariant.