DSP - Operationen zur Signalverschiebung
Verschiebung bedeutet Bewegung des Signals entweder im Zeitbereich (um die Y-Achse) oder im Amplitudenbereich (um die X-Achse). Dementsprechend können wir die Verschiebung in zwei Kategorien einteilen, die als Zeitverschiebung und Amplitudenverschiebung bezeichnet werden. Diese werden nachfolgend erläutert.
Zeitverschiebung
Zeitverschiebung bedeutet Verschiebung von Signalen im Zeitbereich. Mathematisch kann es geschrieben werden als
$$ x (t) \ rightarrow y (t + k) $$Dieser K-Wert kann positiv oder negativ sein. Entsprechend dem Vorzeichen des k-Werts gibt es zwei Arten von Verschiebungen, die als Rechtsverschiebung und Linksverschiebung bezeichnet werden.
Fall 1 (K> 0)
Wenn K größer als Null ist, erfolgt die Verschiebung des Signals im Zeitbereich nach "links". Daher ist diese Art der Verschiebung als Linksverschiebung des Signals bekannt.
Example
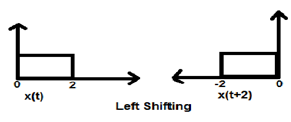
Fall 2 (K <0)
Wenn K kleiner als Null ist, findet die Verschiebung des Signals im Zeitbereich nach rechts statt. Daher wird diese Art der Verschiebung als Rechtsverschiebung bezeichnet.
Example
Die folgende Abbildung zeigt die Verschiebung eines Signals nach rechts um 2.
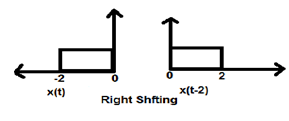
Amplitudenverschiebung
Amplitudenverschiebung bedeutet Signalverschiebung im Amplitudenbereich (um die X-Achse). Mathematisch kann es dargestellt werden als -
$$ x (t) \ rechter Pfeil x (t) + K $$Dieser K-Wert kann positiv oder negativ sein. Dementsprechend haben wir zwei Arten der Amplitudenverschiebung, die nachfolgend diskutiert werden.
Fall 1 (K> 0)
Wenn K größer als Null ist, erfolgt die Signalverschiebung in der x-Achse nach oben. Daher ist diese Art der Verschiebung als Aufwärtsverschiebung bekannt.
Example
Betrachten wir ein Signal x (t), das gegeben ist als;
$$ x = \ begin {Fälle} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {Fälle} $$Nehmen wir K = + 1, damit ein neues Signal geschrieben werden kann als -
$ y (t) \ rightarrow x (t) + 1 $ Also kann y (t) endlich geschrieben werden als;
$$ x (t) = \ begin {Fälle} 1, & t <0 \\ 2, & 0 \ leq t \ leq 2 \\ 1, & t> 0 \ end {Fälle} $$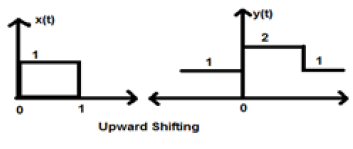
Fall 2 (K <0)
Wenn K kleiner als Null ist, erfolgt eine Signalverschiebung in der X-Achse nach unten. Daher wird es als Abwärtsverschiebung des Signals bezeichnet.
Example
Betrachten wir ein Signal x (t), das gegeben ist als;
$$ x (t) = \ begin {Fälle} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {Fälle} $$Nehmen wir K = -1, damit neues Signal geschrieben werden kann als;
$ y (t) \ rightarrow x (t) -1 $ Also kann y (t) endlich geschrieben werden als;
$$ y (t) = \ begin {Fälle} -1, & t <0 \\ 0, & 0 \ leq t \ leq 2 \\ -1, & t> 0 \ end {Fälle} $$