DSP - Schnelle Fourier-Transformation
In früheren DFT-Methoden haben wir gesehen, dass der rechnerische Teil zu lang ist. Das wollen wir reduzieren. Dies kann durch FFT oder schnelle Fourier-Transformation erfolgen. Wir können also sagen, dass FFT nichts anderes ist als die Berechnung einer diskreten Fourier-Transformation in einem algorithmischen Format, bei dem der rechnerische Teil reduziert wird.
Der Hauptvorteil von FFT besteht darin, dass wir dadurch die FIR-Filter entwerfen können. Mathematisch kann die FFT wie folgt geschrieben werden;
$$ x [K] = \ Anzeigestil \ Summe \ Grenzen_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$Nehmen wir ein Beispiel, um es besser zu verstehen. Wir haben acht Punkte berücksichtigt, die von $ x_0 \ quad bis \ quad x_7 $ benannt sind. Wir werden die geraden Begriffe in einer Gruppe und die ungeraden Begriffe in der anderen Gruppe auswählen. Eine schematische Ansicht des oben Gesagten wurde unten gezeigt -
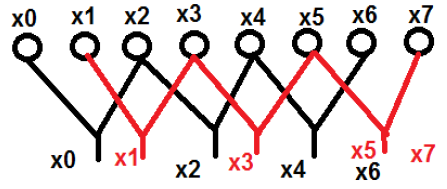
Hier wurden die Punkte x 0 , x 2 , x 4 und x 6 in eine Kategorie eingeteilt, und in ähnlicher Weise wurden die Punkte x 1 , x 3 , x 5 und x 7 in eine andere Kategorie eingeordnet. Jetzt können wir sie weiter in einer Gruppe von zwei machen und mit der Berechnung fortfahren. Lassen Sie uns nun sehen, wie diese Aufteilung in zwei weitere bei der Berechnung hilft.
$ x [k] = \ Anzeigestil \ Summe \ Grenzen_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_N ^ {2rk} + \ Anzeigestil \ Summe \ Grenzen_ {r = 0 } ^ {\ frac {N} {2} -1} x [2r + 1] W_N ^ {(2r + 1) k} $
$ = \ sum_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_ {N / 2} ^ {rk} + \ sum_ {r = 0} ^ {\ frac {N. } {2} -1} x [2r + 1] W_ {N / 2} ^ {rk} \ times W_N ^ k $
$ = G [k] + H [k] \ mal W_N ^ k $
Anfangs haben wir eine Acht-Punkte-Sequenz genommen, aber später haben wir diese in zwei Teile G [k] und H [k] aufgeteilt. G [k] steht für den geraden Teil, während H [k] für den ungeraden Teil steht. Wenn wir es durch ein Diagramm realisieren wollen, dann kann es wie folgt gezeigt werden -
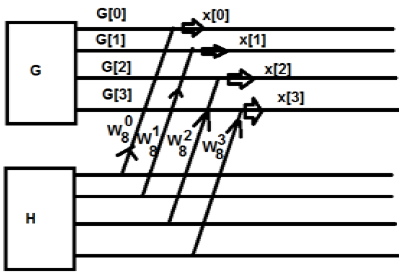
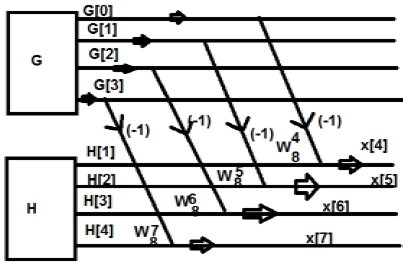
Aus der obigen Abbildung können wir das ersehen
$ W_8 ^ 4 = -1 $
$ W_8 ^ 5 = -W_8 ^ 1 $
$ W_8 ^ 6 = -W_8 ^ 2 $
$ W_8 ^ 7 = -W_8 ^ 3 $
Ebenso können die Endwerte wie folgt geschrieben werden:
$ G [0] -H [0] = x [4] $
$ G [1] -W_8 ^ 1H [1] = x [5] $
$ G [2] -W_8 ^ 2H [2] = x [6] $
$ G [1] -W_8 ^ 3H [3] = x [7] $
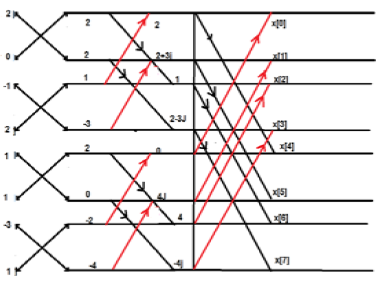
Die obige ist eine periodische Reihe. Der Nachteil dieses Systems ist, dass K nicht über 4 Punkte hinaus gebrochen werden kann. Lassen Sie uns nun das Obige weiter zerlegen. Wir werden die Strukturen so etwas bekommen
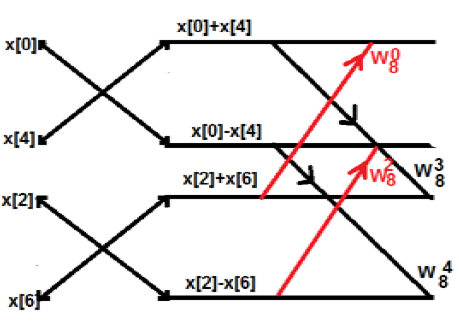
Beispiel
Betrachten Sie die Folge x [n] = {2,1, -1, -3,0,1,2,1}. Berechnen Sie die FFT.
Solution - Die angegebene Sequenz ist x [n] = {2,1, -1, -3,0,1,2,1}
Ordnen Sie die Bedingungen wie unten gezeigt an.