DSP - Operationen zur Signalintegration
Die Integration eines Signals bedeutet die Summierung dieses Signals in einem bestimmten Zeitbereich, um ein modifiziertes Signal zu erhalten. Mathematisch kann dies dargestellt werden als -
$$ x (t) \ rightarrow y (t) = \ int _ {- \ infty} ^ {t} x (t) dt $$Auch hier können wir in den meisten Fällen eine mathematische Integration durchführen und das resultierende Signal finden, aber eine direkte Integration in schneller Folge ist für Signale möglich, die in rechteckigem Format grafisch dargestellt sind. Wie bei der Differenzierung verweisen wir auch hier auf eine Tabelle, um das Ergebnis schnell zu erhalten.
| Ursprüngliches Signal | Integriertes Signal |
|---|---|
| 1 | Impuls |
| Impuls | Schritt |
| Schritt | Rampe |
Beispiel
Betrachten wir ein Signal $ x (t) = u (t) -u (t-3) $. Es ist in Fig. 1 unten gezeigt. Wir können deutlich sehen, dass es sich um ein Schrittsignal handelt. Jetzt werden wir es integrieren. In Bezug auf die Tabelle wissen wir, dass die Integration des Stufensignals ein Rampensignal ergibt.
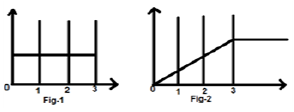
Wir werden es jedoch mathematisch berechnen,
$ y (t) = \ int _ {- \ infty} ^ {t} x (t) dt $
$ = \ int _ {- \ infty} ^ {t} [u (t) -u (t-3)] dt $
$ = \ int _ {- \ infty} ^ {t} u (t) dt- \ int _ {- \ infty} ^ {t} u (t-3) dt $
$ = r (t) -r (t-3) $
Das gleiche ist wie in Fig. 2 gezeigt aufgetragen.