DSP - Klassifizierung von DT-Signalen
Genau wie kontinuierliche Zeitsignale können diskrete Zeitsignale gemäß den Bedingungen oder Operationen an den Signalen klassifiziert werden.
Gerade und ungerade Signale
Gleichmäßiges Signal
Ein Signal wird als gerade oder symmetrisch bezeichnet, wenn es die folgende Bedingung erfüllt:
$$ x (-n) = x (n) $$
Hier können wir sehen, dass x (-1) = x (1), x (-2) = x (2) und x (-n) = x (n). Somit ist es ein gleichmäßiges Signal.
Ungerades Signal
Ein Signal wird als ungerade bezeichnet, wenn es die folgende Bedingung erfüllt:
$$ x (-n) = -x (n) $$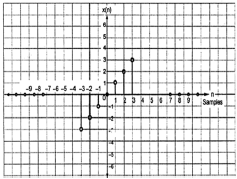
Aus der Figur können wir sehen, dass x (1) = -x (-1), x (2) = -x (2) und x (n) = -x (-n). Daher ist es sowohl ein ungerades als auch ein antisymmetrisches Signal.
Periodische und nichtperiodische Signale
Ein diskretes Zeitsignal ist genau dann periodisch, wenn es die folgende Bedingung erfüllt:
$$ x (n + N) = x (n) $$Hier wiederholt sich das x (n) -Signal nach der N-Periode. Dies kann am besten unter Berücksichtigung eines Kosinussignals verstanden werden -
$$ x (n) = A \ cos (2 \ pi f_ {0} n + \ theta) $$ $$ x (n + N) = A \ cos (2 \ pi f_ {0} (n + N) + \ theta) = A \ cos (2 \ pi f_ {0} n + 2 \ pi f_ {0} N + \ theta) $$ $$ = A \ cos (2 \ pi f_ {0} n + 2 \ pi f_ {0} N + \ theta) $$Damit das Signal periodisch wird, sollte die folgende Bedingung erfüllt sein:
$$ x (n + N) = x (n) $$ $$ \ Rechtspfeil A \ cos (2 \ pi f_ {0} n + 2 \ pi f_ {0} N + \ theta) = A \ cos (2 \ pi f_ {0} n + \ theta) $$dh $ 2 \ pi f_ {0} N $ ist ein ganzzahliges Vielfaches von $ 2 \ pi $
$$ 2 \ pi f_ {0} N = 2 \ pi K $$ $$ \ Rightarrow N = \ frac {K} {f_ {0}} $$Die Frequenzen diskreter sinusförmiger Signale werden durch ein ganzzahliges Vielfaches von $ 2 \ pi $ getrennt.
Energie- und Energiesignale
Energiesignal
Die Energie eines diskreten Zeitsignals wird als E bezeichnet. Mathematisch kann sie geschrieben werden als;
$$ E = \ displaystyle \ sum \ limit_ {n = - \ infty} ^ {+ \ infty} | x (n) | ^ 2 $$Wenn jeder einzelne Wert von $ x (n) $ quadriert und addiert wird, erhalten wir das Energiesignal. Hier ist $ x (n) $ das Energiesignal und seine Energie ist über die Zeit endlich, dh $ 0 <E <\ infty $
Netzsignal
Die durchschnittliche Leistung eines diskreten Signals wird als P dargestellt. Mathematisch kann dies geschrieben werden als;
$$ P = \ lim_ {N \ bis \ infty} \ frac {1} {2N + 1} \ displaystyle \ sum \ limit_ {n = -N} ^ {+ N} | x (n) | ^ 2 $$Hier ist die Leistung endlich, dh 0 <P <∞. Es gibt jedoch einige Signale, die weder zu einem Energie- noch zu einem Leistungssignal gehören.