DSP - Operationen zur Signaldifferenzierung

Zwei sehr wichtige Operationen, die an den Signalen ausgeführt werden, sind Differenzierung und Integration.

Unterscheidung

Die Differenzierung eines Signals x (t) bedeutet eine Steigungsdarstellung dieses Signals in Bezug auf die Zeit. Mathematisch wird es dargestellt als;

$$ x (t) \ rightarrow \ frac {dx (t)} {dt} $$

Bei der OPAMP-Differenzierung ist diese Methode sehr hilfreich. Wir können ein Signal leicht grafisch unterscheiden, anstatt die Formel zu verwenden. Voraussetzung ist jedoch, dass das Signal entweder rechteckig oder dreieckig ist, was in den meisten Fällen der Fall ist.

Ursprüngliches Signal	Differenziertes Signal
Rampe	Schritt
Schritt	Impuls
Impuls	1

Die obige Tabelle zeigt den Zustand des Signals nach der Differenzierung. Beispielsweise wird ein Rampensignal nach der Differenzierung in ein Stufensignal umgewandelt. In ähnlicher Weise wird ein Einheitsschrittsignal zu einem Impulssignal.

Beispiel

Das uns gegebene Signal sei $ x (t) = 4 [r (t) -r (t-2)] $. Wenn dieses Signal aufgezeichnet wird, sieht es wie das auf der linken Seite der unten angegebenen Abbildung aus. Unser Ziel ist es nun, das gegebene Signal zu differenzieren.

Zunächst werden wir die gegebene Gleichung differenzieren. Wir wissen, dass das Rampensignal nach der Differenzierung ein Einheitsschritt-Signal ergibt.

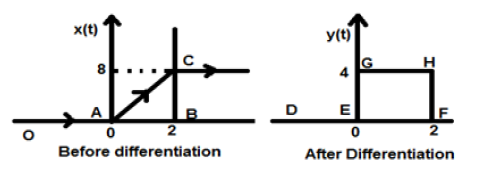
Unser resultierendes Signal y (t) kann also wie folgt geschrieben werden:

$ y (t) = \ frac {dx (t)} {dt} $

$ = \ frac {d4 [r (t) -r (t-2)]} {dt} $

$ = 4 [u (t) -u (t-2)] $

Nun wird schließlich dieses Signal aufgezeichnet, das auf der rechten Seite der obigen Abbildung dargestellt ist.