DSP - Operationen zur Skalierung von Signalen

Skalierung eines Signals bedeutet, dass eine Konstante mit der Zeit oder Amplitude des Signals multipliziert wird.

Zeitskalierung

Wenn eine Konstante mit der Zeitachse multipliziert wird, spricht man von Zeitskalierung. Dies kann mathematisch dargestellt werden als;

$ x (t) \ rechter Pfeil y (t) = x (\ alpha t) $ oder $ x (\ frac {t} {\ alpha}) $; wobei α ≠ 0 ist

Wenn also die y-Achse gleich ist, nimmt die Größe der x-Achse entsprechend dem Vorzeichen der Konstanten (ob positiv oder negativ) ab oder zu. Daher kann die Skalierung auch in zwei Kategorien unterteilt werden, wie nachstehend erläutert wird.

Zeitkomprimierung

Immer wenn Alpha größer als Null ist, wird die Amplitude des Signals durch Alpha geteilt, während der Wert der Y-Achse gleich bleibt. Dies wird als Zeitkomprimierung bezeichnet.

Example

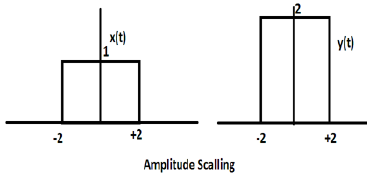
Betrachten wir ein Signal x (t), das wie in der folgenden Abbildung dargestellt ist. Nehmen wir den Wert von Alpha als 2. Also ist y (t) x (2t), was in der angegebenen Abbildung dargestellt ist.

Aus den obigen Abbildungen ist klar ersichtlich, dass die Zeitgröße in der y-Achse gleich bleibt, die Amplitude in der x-Achse jedoch von 4 auf 2 abnimmt. Daher handelt es sich um eine Zeitkomprimierung.

Zeiterweiterung

Wenn die Zeit durch das konstante Alpha geteilt wird, wird die Größe des Signals auf der Y-Achse mit dem Alpha multipliziert, wobei die Größe der X-Achse unverändert bleibt. Daher wird dies als Zeiterweiterungssignal bezeichnet.

Example

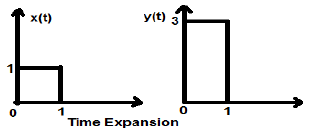
Betrachten wir ein quadratisches Signal x (t) der Größe 1. Wenn wir es zeitlich mit einer Konstanten 3 skalieren, so dass $ x (t) \ rechter Pfeil y (t) \ rechter Pfeil x (\ frac {t} {3}) ) $, dann wird die Amplitude des Signals um das Dreifache geändert, wie in der folgenden Abbildung gezeigt.

Amplitudenskalierung

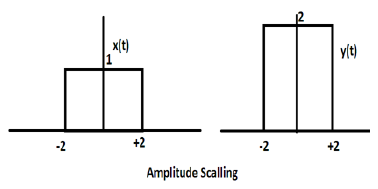
Die Multiplikation einer Konstanten mit der Amplitude des Signals bewirkt eine Amplitudenskalierung. Abhängig vom Vorzeichen der Konstante kann es sich entweder um eine Amplitudenskalierung oder eine Dämpfung handeln. Betrachten wir ein Rechtecksignal x (t) = Π (t / 4).

Angenommen, wir definieren eine andere Funktion y (t) = 2 Π (t / 4). In diesem Fall wird der Wert der y-Achse verdoppelt, wobei der Wert der Zeitachse unverändert bleibt. Das ist in der folgenden Abbildung dargestellt.

Betrachten Sie eine andere Rechteckwellenfunktion, die als z (t) definiert ist, wobei z (t) = 0,5 Π (t / 4) ist. Hier ist die Amplitude der Funktion z (t) halb so groß wie die von x (t), dh die Zeitachse bleibt gleich, die Amplitudenachse wird halbiert. Dies wird durch die folgende Abbildung veranschaulicht.