DSP - Operationen zur Signalfaltung
Die Faltung zweier Signale im Zeitbereich entspricht der Multiplikation ihrer Darstellung im Frequenzbereich. Mathematisch können wir die Faltung zweier Signale als schreiben
$$ y (t) = x_ {1} (t) * x_ {2} (t) $$ $$ = \ int _ {- \ infty} ^ {\ infty} x_ {1} (p) .x_ {2 } (tp) dp $$Schritte zur Faltung
- Nehmen Sie das Signal x 1 (t) und setzen Sie dort t = p, so dass es x 1 (p) ist.
- Nimm das Signal x 2 (t) und mache den Schritt 1 und mache es x 2 (p).
- Machen Sie die Faltung des Signals dh x 2 (-p).
- Führen Sie die Zeitverschiebung des obigen Signals x 2 [- (pt)] durch.
- Führen Sie dann die Multiplikation beider Signale durch. dh $ x_ {1} (p) .x_ {2} [- (p - t)] $
Beispiel
Lassen Sie uns die Faltung eines Schrittsignals u (t) mit seiner eigenen Art durchführen.
$ y (t) = u (t) * u (t) $
$ = \ int _ {- \ infty} ^ {\ infty} [u (p) .u [- (pt)] dp $
Nun kann dieses t größer oder kleiner als Null sein, die in den folgenden Figuren gezeigt sind
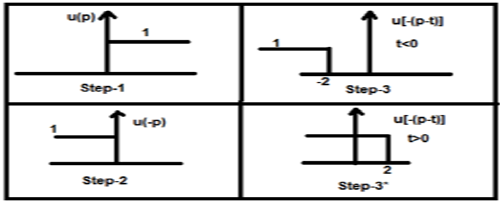
Im obigen Fall ergibt sich das Ergebnis mit folgenden Möglichkeiten
$ y (t) = \ begin {Fälle} 0, & wenn \ quad t <0 \\\ int_ {0} ^ {t} 1dt, & für \ quad t> 0 \ end {Fälle} $
$ = \ begin {Fälle} 0, & if \ quad t <0 \\ t, & t> 0 \ end {Fälle} = r (t) $
Eigenschaften der Faltung
Kommutativ
Es besagt, dass die Reihenfolge der Faltung keine Rolle spielt, was mathematisch als dargestellt werden kann
$$ x_ {1} (t) * x_ {2} (t) = x_ {2} (t) * x_ {1} (t) $$Assoziativ
Es besagt, dass die Reihenfolge der Faltung mit drei Signalen alles sein kann. Mathematisch kann es gezeigt werden als;
$$ x_ {1} (t) * [x_ {2} (t) * x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t)] * x_ {3} (t) $$Verteilend
Zuerst können zwei Signale hinzugefügt werden, und dann kann ihre Faltung zum dritten Signal erfolgen. Dies entspricht der Faltung zweier Signale einzeln mit dem dritten Signal, die schließlich addiert werden. Mathematisch kann dies geschrieben werden als;
$$ x_ {1} (t) * [x_ {2} (t) + x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t) + x_ {1} ( t) * x_ {3} (t)] $$Bereich
Wenn ein Signal das Ergebnis der Faltung zweier Signale ist, ist die Fläche des Signals die Multiplikation dieser einzelnen Signale. Mathematisch kann dies geschrieben werden
Wenn $ y (t) = x_ {1} * x_ {2} (t) $
Dann ist Fläche von y (t) = Fläche von x 1 (t) X Fläche von x 2 (t)
Skalierung
Wenn zwei Signale auf eine unbekannte Konstante "a" skaliert werden und die Faltung erfolgt, wird das resultierende Signal ebenfalls auf dieselbe Konstante "a" gefaltet und durch diese Größe geteilt, wie unten gezeigt.
Wenn $ x_ {1} (t) * x_ {2} (t) = y (t) $
Dann ist $ x_ {1} (at) * x_ {2} (at) = \ frac {y (at)} {a}, a \ ne 0 $
Verzögern
Angenommen, ein Signal y (t) ist ein Ergebnis der Faltung zweier Signale x1 (t) und x2 (t). Wenn die beiden Signale um die Zeit t1 bzw. t2 verzögert sind, wird das resultierende Signal y (t) um (t1 + t2) verzögert. Mathematisch kann es geschrieben werden als -
Wenn $ x_ {1} (t) * x_ {2} (t) = y (t) $
Dann ist $ x_ {1} (t-t_ {1}) * x_ {2} (t-t_ {2}) = y [t- (t_ {1} + t_ {2})] $
Gelöste Beispiele
Example 1 - Finden Sie die Faltung der Signale u (t-1) und u (t-2).
Solution- Gegebene Signale sind u (t-1) und u (t-2). Ihre Faltung kann wie unten gezeigt erfolgen -
$ y (t) = u (t-1) * u (t-2) $
$ y (t) = \ int _ {- \ infty} ^ {+ \ infty} [u (t-1) .u (t-2)] dt $
$ = r (t-1) + r (t-2) $
$ = r (t-3) $
Example 2 - Finden Sie die Faltung von zwei Signalen gegeben durch
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$ x_ {2} (n) = \ begin {Fälle} 2, & 0 \ leq n \ leq 4 \\ 0, & x> anderswo \ end {Fälle} $
Solution - -
x 2 (n) kann als $ x_ {2} (n) = \ lbrace 2,2,2,2,2 \ rbrace Originalfirst $ dekodiert werden
x 1 (n) ist zuvor $ = \ lbrace 3, -2,3 \ rbrace = 3-2Z ^ {- 1} + 2Z ^ {- 2} $ gegeben
In ähnlicher Weise ist $ x_ {2} (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4} $
Resultierendes Signal,
$ X (Z) = X_ {1} (Z) X_ {2} (z) $
$ = \ lbrace 3-2Z ^ {- 1} + 2Z ^ {- 2} \ rbrace \ times \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {-4} \ rbrace $
$ = 6 + 2Z ^ {- 1} + 6Z ^ {- 2} + 6Z ^ {- 3} + 6Z ^ {- 4} + 6Z ^ {- 5} $
Wenn wir die obige inverse Z-Transformation nehmen, erhalten wir das resultierende Signal als
$ x (n) = \ lbrace 6,2,6,6,6,0,4 \ rbrace $ Origin am ersten
Example 3 - Bestimmen Sie die Faltung der folgenden 2 Signale -
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution - -
Wenn wir die Z-Transformation der Signale nehmen, erhalten wir:
$ x (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 3} $
Und $ h (n) = 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} $
Die Faltung zweier Signale bedeutet nun die Multiplikation ihrer Z-Transformationen
Das ist $ Y (Z) = X (Z) \ mal h (Z) $
$ = \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 3} \ rbrace \ times \ lbrace 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} \ rbrace $
$ = \ lbrace 2 + 5Z ^ {- 1} + 8Z ^ {- 2} + 6Z ^ {- 3} + 3Z ^ {- 4} + 3Z ^ {- 5} + Z ^ {- 6} \ rbrace $
Unter Verwendung der inversen Z-Transformation kann das resultierende Signal wie folgt geschrieben werden:
$ y (n) = \ lbrace 2,5,8,6,6,1 \ rbrace Originalfirst $