DSP - Klassifizierung von CT-Signalen

Kontinuierliche Zeitsignale können nach verschiedenen Bedingungen oder Operationen klassifiziert werden, die an den Signalen ausgeführt werden.

Gerade und ungerade Signale

Gleichmäßiges Signal

Ein Signal soll auch dann sein, wenn es die folgende Bedingung erfüllt;

$$ x (-t) = x (t) $$

Die zeitliche Umkehrung des Signals bedeutet hier keine Änderung der Amplitude. Betrachten Sie zum Beispiel die unten gezeigte Dreieckswelle.

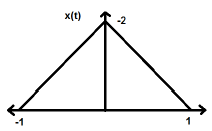
Das Dreieckssignal ist ein gerades Signal. Da es um die Y-Achse symmetrisch ist. Wir können sagen, es ist ein Spiegelbild um die Y-Achse.

Betrachten Sie ein anderes Signal wie in der folgenden Abbildung gezeigt.

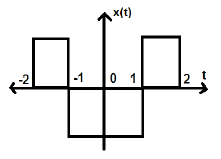
Wir können sehen, dass das obige Signal gerade ist, da es symmetrisch zur Y-Achse ist.

Ungerades Signal

Ein Signal wird als ungerade bezeichnet, wenn es die folgende Bedingung erfüllt

$$ x (-t) = -x (t) $$

Hier findet sowohl die Zeitumkehr als auch die Amplitudenänderung gleichzeitig statt.

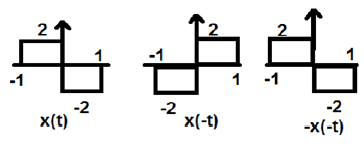
In der obigen Abbildung sehen wir ein Schrittsignal x (t). Um zu testen, ob es sich um ein ungerades Signal handelt oder nicht, führen wir zuerst die Zeitumkehrung durch, dh x (-t), und das Ergebnis ist wie in der Abbildung gezeigt. Dann kehren wir die Amplitude des resultierenden Signals um, dh –x (-t), und wir erhalten das Ergebnis wie in der Abbildung gezeigt.

Wenn wir die erste und die dritte Wellenform vergleichen, können wir sehen, dass sie gleich sind, dh x (t) = -x (-t), was unsere Kriterien erfüllt. Daher ist das obige Signal ein ungerades Signal.

Einige wichtige Ergebnisse in Bezug auf gerade und ungerade Signale sind unten angegeben.

Gerade × Gerade = Gerade
Ungerade × Ungerade = Gerade
Gerade × ungerade = ungerade
Gerade ± Gerade = Gerade
Ungerade ± Ungerade = Ungerade
Gerade ± ungerade = weder gerade noch ungerade

Darstellung eines Signals in gerader oder ungerader Form

Einige Signale können nicht direkt in gerade oder ungerade Typen eingeteilt werden. Diese werden als Kombination von geraden und ungeraden Signalen dargestellt.

$$ x (t) \ rightarrow x_ {e} (t) + x_ {0} (t) $$

Wobei x _e (t) das gerade Signal darstellt und x _o (t) das ungerade Signal darstellt

$$ x_ {e} (t) = \ frac {[x (t) + x (-t)]} {2} $$

Und

$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$

Beispiel

Finden Sie die geraden und ungeraden Teile des Signals $ x (n) = t + t ^ {2} + t ^ {3} $

Solution - Durch Umkehren von x (n) erhalten wir

$$ x (-n) = -t + t ^ {2} -t ^ {3} $$

Nun, nach Formel, der gerade Teil

$$ x_ {e} (t) = \ frac {x (t) + x (-t)} {2} $$

$$ = \ frac {[(t + t ^ {2} + t ^ {3}) + (- t + t ^ {2} -t ^ {3})]} {2} $$

$$ = t ^ {2} $$

In ähnlicher Weise ist gemäß der Formel der ungerade Teil

$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$

$$ = \ frac {[(t + t ^ {2} + t ^ {3}) - (- t + t ^ {2} -t ^ {3})]} {2} $$

$$ = t + t ^ {3} $$

Periodische und nichtperiodische Signale

Periodische Signale

Das periodische Signal wiederholt sich nach einem bestimmten Zeitintervall. Wir können dies in Gleichungsform zeigen als -

$$ x (t) = x (t) \ pm nT $$

Wobei n = eine ganze Zahl (1,2,3 ……)

T = Grundzeitraum (FTP) ≠ 0 und ≠ ≠

Die fundamentale Zeitspanne (FTP) ist der kleinste positive und feste Zeitwert, für den das Signal periodisch ist.

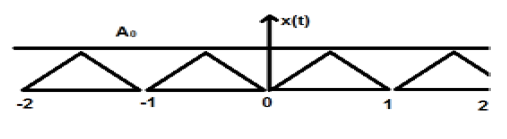
In der obigen Abbildung der Amplitude A ist ein dreieckiges Signal dargestellt. Hier wiederholt sich das Signal alle 1 Sekunde. Daher können wir sagen, dass das Signal periodisch ist und sein FTP 1 Sek. Beträgt.

Nichtperiodisches Signal

Wir können einfach sagen, dass die Signale, die nicht periodisch sind, nicht periodischer Natur sind. Es ist offensichtlich, dass sich diese Signale nach keiner Intervallzeit wiederholen.

Nichtperiodische Signale folgen keinem bestimmten Format. daher kann keine bestimmte mathematische Gleichung sie beschreiben.

Energie- und Energiesignale

Ein Signal wird genau dann als Energiesignal bezeichnet, wenn die enthaltene Gesamtenergie endlich und ungleich Null ist (0 <E <∞). Daher ist für jedes Energietypsignal das gesamte normalisierte Signal endlich und ungleich Null.

Ein sinusförmiges Wechselstromsignal ist ein perfektes Beispiel für ein Signal vom Energietyp, da es sich in einem Fall in einer positiven Halbwelle befindet und in der nächsten Halbwelle dann negativ ist. Daher wird seine durchschnittliche Leistung Null.

Ein verlustfreier Kondensator ist auch ein perfektes Beispiel für ein Signal vom Energietyp, da es, wenn es an eine Quelle angeschlossen ist, bis zu seinem optimalen Pegel aufgeladen wird und wenn die Quelle entfernt wird, diese gleiche Energiemenge durch eine Last abführt und ihre durchschnittliche Leistung auf erzeugt Null.

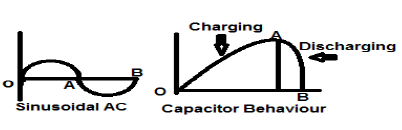
Für jedes endliche Signal x (t) kann die Energie als E symbolisiert werden und wird geschrieben als;

$$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$

Die spektrale Dichte von Signalen vom Energietyp gibt die Energiemenge an, die auf verschiedenen Frequenzniveaus verteilt ist.

Leistungssignale

Ein Signal wird genau dann als Leistungssignal bezeichnet, wenn die normalisierte Durchschnittsleistung endlich und ungleich Null ist, dh (0 <p <∞). Für ein Signal vom Leistungstyp ist die normalisierte Durchschnittsleistung endlich und ungleich Null. Fast alle periodischen Signale sind Leistungssignale und ihre durchschnittliche Leistung ist endlich und ungleich Null.

In mathematischer Form kann die Potenz eines Signals x (t) wie folgt geschrieben werden:

$$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$

Unterschied zwischen Energie- und Leistungssignalen

Die folgende Tabelle fasst die Unterschiede zwischen Energie- und Leistungssignalen zusammen.

Netzsignal	Energiesignal
Praktische periodische Signale sind Leistungssignale.	Nichtperiodische Signale sind Energiesignale.
Hier ist die normalisierte Durchschnittsleistung endlich und ungleich Null.	Hier ist die gesamte normalisierte Energie endlich und ungleich Null.
Mathematisch, $$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$	Mathematisch, $$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$
Das Vorhandensein dieser Signale ist im Laufe der Zeit unendlich.	Diese Signale existieren für einen begrenzten Zeitraum.
Die Energie des Leistungssignals ist über die unendliche Zeit unendlich.	Die Leistung des Energiesignals ist über unendliche Zeit Null.

Gelöste Beispiele

Example 1 - Finden Sie die Potenz eines Signals $ z (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) + 4 \ sin (3 \ Pi + 30 ^ {o}) $

Solution- Die beiden obigen Signale sind orthogonal zueinander, da ihre Frequenzterme identisch sind und sie auch die gleiche Phasendifferenz aufweisen. Die Gesamtmacht ist also die Summe der Einzelkräfte.

Sei $ z (t) = x (t) + y (t) $

Wobei $ x (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) $ und $ y (t) = 4 \ sin (3 \ Pi + 30 ^ {o}) $

Potenz von $ x (t) = \ frac {2 ^ {2}} {2} = 2 $

Potenz von $ y (t) = \ frac {4 ^ {2}} {2} = 8 $

Daher ist $ P (z) = p (x) + p (y) = 2 + 8 = 10 $ … Ans.

Example 2 - Testen Sie, ob das Signal mit $ x (t) = t ^ {2} + j \ sin t $ konjugiert ist oder nicht?

Solution- Hier ist der Realteil t ² gerade und der ungerade Teil (imaginär) $ \ sin t $ ungerade. Das obige Signal ist also ein konjugiertes Signal.

Example 3 - Überprüfen Sie, ob $ X (t) = \ sin \ omega t $ ein ungerades oder ein gerades Signal ist.

Solution - Gegeben $ X (t) = \ sin \ omega t $

Durch die Zeitumkehr erhalten wir $ \ sin (- \ omega t) $

Aber wir wissen, dass $ \ sin (- \ phi) = - \ sin \ phi $.

Deshalb,

$$ \ sin (- \ omega t) = - \ sin \ omega t $$

Dies erfüllt die Bedingung, dass ein Signal ungerade ist. Daher ist $ \ sin \ omega t $ ein ungerades Signal.