सांख्यिकी - बीटा वितरण
बीटा वितरण दो सकारात्मक आकार मापदंडों द्वारा निरंतर संभाव्यता वितरण का प्रतिनिधित्व करता है, $ \alpha $ तथा $ \beta $, जो यादृच्छिक चर x के प्रतिपादक के रूप में प्रकट होते हैं और वितरण के आकार को नियंत्रित करते हैं।
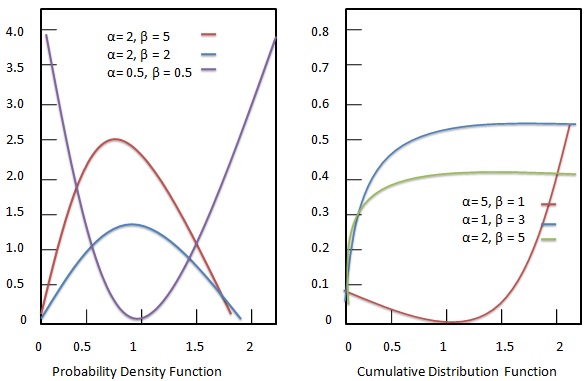
संभाव्यता घनत्व कार्य
बीटा वितरण की संभाव्यता घनत्व कार्य निम्नानुसार दिया गया है:
सूत्र
कहाँ -
${ \alpha, \beta }$ = आकार मापदंडों।
${a, b}$ = ऊपरी और निचले सीमा।
${B(\alpha,\beta)}$ = बीटा फ़ंक्शन।
मानक बीटा वितरण
1 और 0 के रूप में ऊपरी और निचले सीमा होने के मामले में, बीटा वितरण को मानक बीटा वितरण कहा जाता है। यह निम्नलिखित सूत्र द्वारा संचालित है:
सूत्र
संचयी वितरण फलन
बीटा वितरण का संचयी वितरण कार्य निम्नानुसार है:
सूत्र
कहाँ -
${ \alpha, \beta }$ = आकार मापदंडों।
${a, b}$ = ऊपरी और निचले सीमा।
${B(\alpha,\beta)}$ = बीटा फ़ंक्शन।
इसे अधूरा बीटा फ़ंक्शन अनुपात भी कहा जाता है।