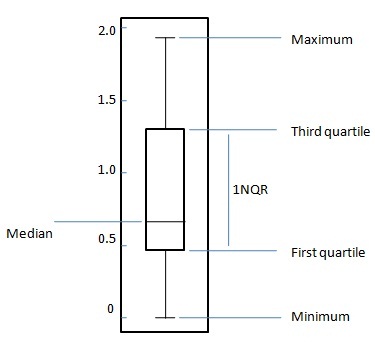
सांख्यिकी - बॉक्सप्लाट्स

बॉक्स प्लॉट पांच नंबर सारांश के आधार पर डेटा के वितरण को प्रदर्शित करने के लिए एक मानकीकृत तरीका है।

1. Minimum

2. पहला चतुर्थांश

3. Median

4. तीसरा चौकड़ी

5. Maximum

बॉक्स प्लॉट आरेख में एक समान रूप से वितरित डेटा सेट के लिए, केंद्रीय आयत पहली चतुर्थक को तीसरी चतुर्थक (या इंटरक्वेर्टाइल रेंज, IQR) तक फैलाता है। आयत के अंदर की एक रेखा, माध्यिका और "मूंछ" को दिखाती है, जिसके नीचे और नीचे बॉक्स में न्यूनतम और अधिकतम मानों के स्थान दिखाई देते हैं। इस तरह का बॉक्स प्लॉट न्यूनतम से भिन्नता की पूरी श्रृंखला, भिन्नता की संभावना सीमा, आईक्यूआर और माध्यिका को प्रदर्शित करता है।

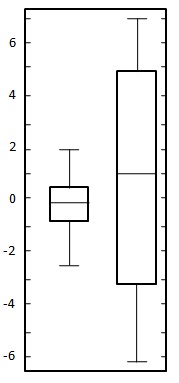
समस्या का विवरण:

निम्नलिखित दो डेटासेट के लिए एक बॉक्स प्लॉट बनाएं।

0.22
-0.87
-2.39
-1.79
0.37
-1.54
1.28
-0.31
-0.74
1.72
0.38
-0.17
-0.62
-1.10
0.30
0.15
2.30
0.19
-0.50
-0.09

-5.13
-2.19
-2.43
-3.83
0.50
-3.25
4.32
1.63
5.18
-0.43
7.11
4.87
-3.10
-5.81
3.76
6.31
2.58
0.07
5.76
3.50

उपाय:

यहां दोनों डेटासेट समान रूप से शून्य के आसपास संतुलित हैं, इसलिए माध्य शून्य के आसपास है। पहले डेटा सेट में भिन्नता -2.5 से 2.5 के बीच होती है जबकि दूसरे डेटा सेट में लगभग -6 से लेकर 6. तक होती है। जैसा कि नीचे दिखाया गया है चार्ट तैयार करें: