सांख्यिकी - गामा वितरण

गामा वितरण दो-पैरामीटर परिवार के निरंतर संभाव्यता वितरण का प्रतिनिधित्व करता है। गामा वितरण आमतौर पर तीन प्रकार के पैरामीटर संयोजनों के साथ तैयार किया जाता है।

एक आकार पैरामीटर $ k $ और एक स्केल पैरामीटर $ the थीटा $।
एक आकार पैरामीटर $ \ अल्फा = के $ और एक व्युत्क्रम स्केल पैरामीटर $ \ बीटा = \ frac {1} {\ थीटा} $, जिसे रेट पैरामीटर कहा जाता है।
एक आकार पैरामीटर $ k $ और माध्य पैरामीटर $ \ mu = \ frac {k} {\ beta} $।

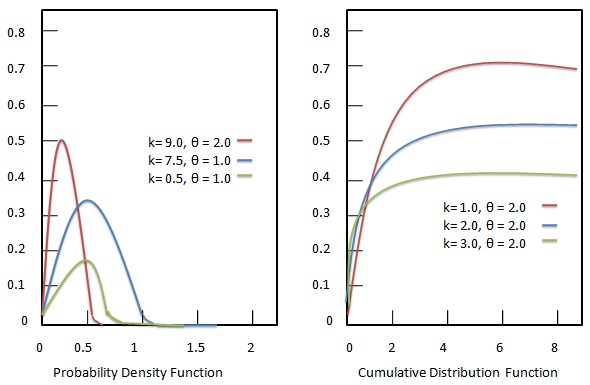
प्रत्येक पैरामीटर एक सकारात्मक वास्तविक संख्या है। गामा वितरण निम्नलिखित मानदंडों द्वारा संचालित अधिकतम एन्ट्रापी संभावना वितरण है।

सूत्र

$ {E [X] = k \ theta = \ frac {\ अल्फा} {\ बीटा} \ gt 0 \ और \ is \ निश्चित। \\ [7pt] E [ln (X)] = \ psi (k) + ln (\ theta) = \ psi (\ अल्फा) - ln (\ Beta) \ और \ is \ निश्चित है। } $

कहाँ -

$ {X} $ = यादृच्छिक चर।
$ {\ psi} $ = डिगामा फ़ंक्शन।

आकार $ \ अल्फा $ और दर $ \ बीटा $ का उपयोग करके विशेषता

संभाव्यता घनत्व कार्य

गामा वितरण की संभाव्यता घनत्व कार्य निम्नानुसार दिया गया है:

सूत्र

$ {f (x; \ अल्फा, \ बीटा) = \ frac {\ बीटा ^ \ अल्फा एक्स ^ {\ अल्फा - 1} ई ^ {- x \ बीटा}} {\ गामा (\ अल्फा)} \ _ \ _ \ ge 0 \ और \ अल्फा, \ Beta \ gt 0} $

कहाँ -