सांख्यिकी - कर्टोसिस

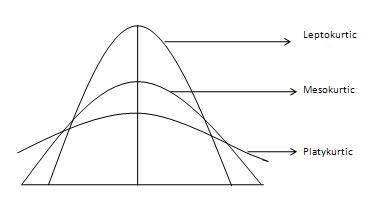
किसी वितरण की थकान की डिग्री को कर्टोसिस द्वारा मापा जाता है। यह हमें बताता है कि वितरण सामान्य वितरण की तुलना में अधिक या कम आउटलाइयर-प्रोन (भारी या हल्का-पूंछ वाला) है। इन्वेस्टोपेडिया के सौजन्य से तीन अलग-अलग प्रकार के घटता, निम्नानुसार दिखाए गए हैं -

घनत्व भूखंडों (बाएं पैनल) से विभिन्न प्रकार के कुर्तोसिस को समझना मुश्किल है, क्योंकि वितरण के लिए पूंछ शून्य के करीब हैं। लेकिन पूंछ में अंतर सामान्य मात्रात्मक-क्वांटाइल भूखंडों (दाएं पैनल) में देखना आसान है।

सामान्य वक्र को मेसोकोर्टिक वक्र कहा जाता है। यदि किसी वितरण की वक्र सामान्य या मेसोकोर्टिक वक्र की तुलना में अधिक बाहरी प्रवण (या भारी-पूंछ वाली) है, तो इसे लेप्टोकर्टिक वक्र कहा जाता है। यदि कोई वक्र सामान्य वक्र की तुलना में कम बाहरी प्रवण (या हल्का-पूंछ वाला) होता है, तो इसे प्लेटिकुरेटर वक्र कहा जाता है। कर्टोसिस को क्षणों द्वारा मापा जाता है और निम्नलिखित सूत्र द्वारा दिया जाता है -

सूत्र

$ {\ Beta_2 = \ frac {\ mu_4} {\ mu_2}} $

कहाँ -

$ {\ mu_4 = \ frac {\ _ (x- \ bar x) ^ 4} {N}} $

अधिक से अधिक नुकीला या लेप्टोकोर्टिक वक्र \ बीटा 2 का मान। एक सामान्य वक्र में 3 का मान होता है, एक लेप्टोक्यूरिक का \ बीटा 2 से अधिक 3 होता है और प्लैटीक्यूरिक का \ बीटा 2 कम होता है तो 3 का।

उदाहरण

Problem Statement:

एक कारखाने के 45 श्रमिकों के दैनिक वेतन पर डेटा दिया जाता है। माध्य के बारे में क्षण का उपयोग करके \ Beta_1 और \ beta_2 की गणना करें। परिणामों पर टिप्पणी करें।

मजदूरी (रु।)	श्रमिकों की संख्या
100-200	1
120-200	2
140-200	6
160-200	20
180-200	1 1
200-200	3
220-200	2

Solution:

मजदूरी (रु।)	श्रमिकों की संख्या (एफ)	मध्य-पीटी मीटर	m - $ {\ frac {170} {20}} $ d	$ {} $ Fd	$ {Fd ^ 2} $	$ {Fd ^ 3} $	$ {Fd ^ 4} $
100-200	1	110	-3	-3	9	-27	81
120-200	2	130	-2	-4	8	-16	32
140-200	6	150	-1	-6	6	-6	6
160-200	20	170	0	0	0	0	0
180-200	1 1	190	1	1 1	1 1	1 1	1 1
200-200	3	210	2	6	12	24	48
220-200	2	230	3	6	18	54	162
	$ {एन = 45} $			$ {\ _ fd = 10} $	$ {\ _ fd ^ 2 = 64} $	$ {\ sum fd ^ 3 = 40} $	$ {\ sum fd ^ 4 = 330} $

चूँकि विचलन एक ग्रहण किए गए माध्य से लिया गया है, इसलिए हम पहले मनमानी उत्पत्ति के बारे में और फिर माध्य के बारे में क्षणों की गणना करते हैं। मनमानी उत्पत्ति के बारे में क्षण '170'

$ {\ mu_1 ^ 1 = \ frac {\ sum fd} {N} \ टाइम्स i = \ frac {10} {45} \ गुना 20 = 4.44 \\ [7pt] \ mu_2 ^ 1 = \ frac / \ sum fd ^ 2} {N} \ टाइम्स i ^ 2 = \ frac {64} {45} \ गुना 20 ^ 2 = 568.88 \\ [7pt] \ mu_3 ^ 1 = \ frac {\ _d fd ^ 2} [N} \ _ टाइम्स i ^ 3 = \ frac {40} {45} \ गुना 20 ^ 3 = 7111.11 \\ [7pt] \ mu_4 ^ 1 = \ frac {\ _d fd ^ 4} {N} \ टाइम्स i ^ 4 / \ frac {330} {45} \ गुना 20 ^ 4 = 1173333.33} $

मतलब के बारे में क्षण

$ {\ mu_2 = \ mu'_2 - (\ mu'_1) ^ 2 = 568.88- (4.44) ^ 2 = 549.16 \\ [7pt] \ mu_3 = \ mu'3/3 (3 (\ mu'_1) (\) mu'_2) + 2 (\ mu'_1) ^ 3 \\ [7pt] \, = 7111.11 - (4.44) (568.88) + 2 (4.44) ^ 3 \\ [7pt] \, = 7111.11 - 7577.48 + 175.05 = - 291.32 \\ [7pt] \\ [7pt] \ mu_4 = \ mu'_4 - 4 (\ mu'_1) (\ mu'_3) + 6 (\ mu_1) 2: (2 mu'_2) -3 ((mu'_1) ^ 4 \\ [7pt] \, = 1173333.33 - 4 (4.44) (7111.11) +6 (4.44) ^ 2 (568.88) - 3 (4.44) ^ 4-26 [7pt] \, = 1173333.33 - 126293.31 + 67288.03-1165.87 \\ [7pt] \, = 1113162.18} $

मतलब के बारे में आंदोलन के मूल्य से, अब हम $ {\ beta_1} $ और $ {\ beta_2} $ की गणना कर सकते हैं:

$ {\ beta_1 = \ mu ^ 2_3 = \ frac {(291.32) ^ 2} {(549.16) ^ 3} = 0.00051 \\ [7pt] \ Beta_2 = \ frac \ {mu_4} {(\ mu_2) ^ 2 } = \ frac {1113162.18} {(546.16) ^ 2} = 3.69} $

उपरोक्त गणनाओं से, यह निष्कर्ष निकाला जा सकता है कि $ {\ beta_1} $, जो तिरछापन को मापता है, लगभग शून्य है, जिससे यह संकेत मिलता है कि वितरण लगभग सममित है। $ {\ Beta_2} $ किन उपायों में कर्टोसिस होता है, जिसका मूल्य 3 से अधिक है, इस प्रकार इसका अर्थ है कि वितरण लेप्टोकर्टिक है।