सांख्यिकी - संचयी पॉसों वितरण
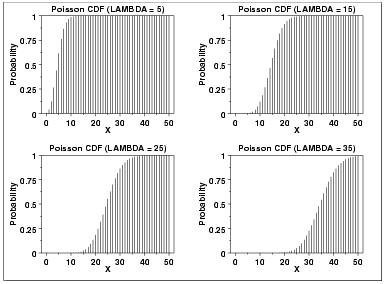
$ {\ lambda} $ आकार पैरामीटर है जो दिए गए समय अंतराल में घटनाओं की औसत संख्या को इंगित करता है। निम्नलिखित $ {\ lambda} $ के चार मूल्यों के लिए पॉइसन संभाव्यता घनत्व फ़ंक्शन का प्लॉट है। संचयी वितरण फलन।
सूत्र
$ $ {F (x, \ lambda) = \ sum_ {k = 0} ^ x \ frac {e ^ {- \ lambda} \ lambda ^ x} {k!}} $ $!
कहाँ -
$ {e} $ = प्राकृतिक लघुगणक का आधार 2.71828 के बराबर है
$ {k} $ = किसी घटना के घटने की संख्या; जिसकी संभावना फ़ंक्शन द्वारा दी गई है।
$ {k!} $ = k का भाज्य
$ {\ lambda} $ = एक सकारात्मक वास्तविक संख्या, दिए गए अंतराल के दौरान होने वाली अपेक्षित संख्या के बराबर
उदाहरण
Problem Statement:
एक जटिल सॉफ्टवेयर सिस्टम प्रति कोड 5,000 लाइनों की 7 त्रुटियों को औसत करता है। कोड की यादृच्छिक रूप से चयनित लाइनों में से 5,000 लाइनों में ठीक 2 त्रुटियों की संभावना क्या है?
Solution:
कोड की यादृच्छिक रूप से चयनित लाइनों की 5,000 लाइनों में ठीक 2 त्रुटियों की संभावना है: