सांख्यिकी - ची-चुकता वितरण
चि-स्क्वार्ड वितरण (ची-वर्ग या $ {X ^ 2} $ - वितरण) स्वतंत्रता की डिग्री के साथ, कश्मीर स्वतंत्र मानक सामान्य यादृच्छिक चर के वर्गों के योग का वितरण है। यह आँकड़ों में सबसे अधिक व्यापक रूप से उपयोग की जाने वाली संभावना वितरण में से एक है। यह गामा वितरण का एक विशेष मामला है।
ची-वर्गीय वितरण का उपयोग सांख्यिकीविदों द्वारा व्यापक रूप से निम्नलिखित की गणना करने के लिए किया जाता है:
नमूना मानक विचलन का उपयोग करके सामान्य वितरण के जनसंख्या मानक विचलन के लिए आत्मविश्वास अंतराल का अनुमान।
कई गुणात्मक चर के वर्गीकरण के दो मानदंडों की स्वतंत्रता की जांच करना।
श्रेणीबद्ध चर के बीच संबंधों की जांच करने के लिए।
नमूना विचरण का अध्ययन करने के लिए जहां अंतर्निहित वितरण सामान्य है।
अपेक्षित और देखी गई आवृत्तियों के बीच अंतर के विचलन का परीक्षण करने के लिए।
ची-स्क्वायर टेस्ट (फिट टेस्ट की एक अच्छाई) का संचालन करने के लिए।
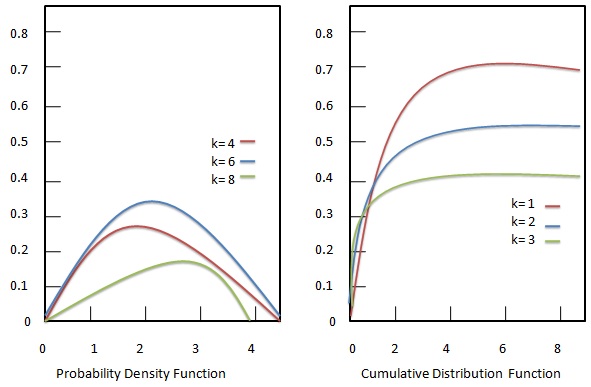
संभाव्यता घनत्व कार्य
ची-स्क्वायर वितरण की संभाव्यता घनत्व कार्य निम्नानुसार दिया गया है:
सूत्र
कहाँ -
$ {\ Gamma (\ frac {k} {2})} $ = गामा फ़ंक्शन पूर्णांक मानों के लिए बंद फॉर्म वैल्यू वाले होते हैं।
$ {x} $ = यादृच्छिक चर।
$ {k} $ = पूर्णांक पैरामीटर।
संचयी वितरण फलन
ची-स्क्वायर वितरण का संचयी वितरण कार्य निम्नानुसार है:
सूत्र
कहाँ -
$ {\ gamma (s, t)} $ = कम अधूरा गामा फ़ंक्शन।
$ {P (s, t)} $ = नियमित गामा कार्य।
$ {x} $ = यादृच्छिक चर।
$ {k} $ = पूर्णांक पैरामीटर।