सांख्यिकी - अवशिष्ट विश्लेषण

अवशिष्ट विश्लेषण का उपयोग अवशिष्ट को परिभाषित करके और अवशिष्ट अवगुणों की जांच करके एक रेखीय प्रतिगमन मॉडल की उपयुक्तता का आकलन करने के लिए किया जाता है।

अवशिष्ट

अवशिष्ट ($ e $) प्रेक्षित मान ($ y $) बनाम अनुमानित मूल्य ($ \ hat y $) के बीच के अंतर को संदर्भित करता है। प्रत्येक डेटा बिंदु में एक अवशिष्ट होता है।

अवशिष्ट प्लॉट

एक अवशिष्ट भूखंड एक ग्राफ है जिसमें अवशिष्ट tthe ऊर्ध्वाधर अक्ष पर होते हैं और स्वतंत्र चर क्षैतिज अक्ष पर होता है। यदि डॉट्स क्षैतिज अक्ष के चारों ओर बेतरतीब ढंग से बिखरे हुए हैं, तो एक रेखीय प्रतिगमन मॉडल डेटा के लिए उपयुक्त है; अन्यथा, एक गैर-रेखीय मॉडल चुनें।

अवशिष्ट प्लॉट के प्रकार

निम्नलिखित उदाहरण अवशिष्ट भूखंडों में कुछ पैटर्न दिखाते हैं।

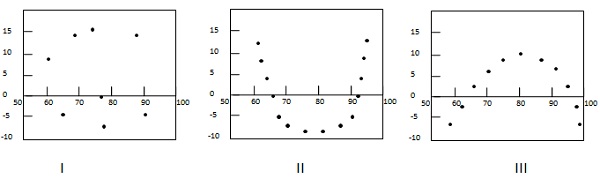
पहले मामले में, डॉट्स को बेतरतीब ढंग से फैलाया जाता है। इसलिए रैखिक प्रतिगमन मॉडल को प्राथमिकता दी जाती है। दूसरे और तीसरे मामले में, डॉट्स गैर-यादृच्छिक रूप से छितरी हुई हैं और बताती हैं कि एक गैर-रेखीय प्रतिगमन विधि पसंद की जाती है।

उदाहरण

Problem Statement:

जांचें कि निम्नलिखित डेटा के लिए एक रैखिक प्रतिगमन मॉडल कहां उपयुक्त है।

$ x $	60	70	80	85	95
$ y $ (वास्तविक मूल्य)	70	65	70	95	85
$ \ hat y $ (अनुमानित मूल्य)	65.411	71.849	78.288	81.507	87.945

Solution:

Step 1: प्रत्येक डेटा बिंदु के लिए अवशिष्टों की गणना करें।

$ x $	60	70	80	85	95
$ y $ (वास्तविक मूल्य)	70	65	70	95	85
$ \ hat y $ (अनुमानित मूल्य)	65.411	71.849	78.288	81.507	87.945
$ ई $ (अवशिष्ट)	4.589	-6.849	-8.288	13.493	-2.945

Step 2: - अवशिष्ट प्लॉट ग्राफ को ड्रा करें।

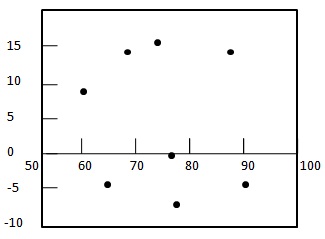
Step 3: - अवशिष्टों की यादृच्छिकता की जाँच करें।

यहाँ अवशिष्ट भूखंड एक यादृच्छिक पैटर्न निकालता है - पहला अवशिष्ट धनात्मक है, दो निम्न ऋणात्मक हैं, चौथा एक धनात्मक है, और अंतिम अवशिष्ट ऋणात्मक है। जैसा कि पैटर्न काफी यादृच्छिक है जो इंगित करता है कि उपरोक्त डेटा के लिए एक रेखीय प्रतिगमन मॉडल उपयुक्त है।