सांख्यिकी - लॉजिस्टिक प्रतिगमन
लॉजिस्टिक रिग्रेशन एक डेटासेट का विश्लेषण करने के लिए एक सांख्यिकीय पद्धति है जिसमें एक या एक से अधिक स्वतंत्र चर होते हैं जो एक परिणाम निर्धारित करते हैं। परिणाम एक द्विभाजित चर के साथ मापा जाता है (जिसमें केवल दो संभावित परिणाम हैं)।
सूत्र
$ {\ pi (x) = \ frac {e ^ {\ Alpha + \ Beta x}} {1 + e ^ {\ Alpha + \ beta x}}} $
कहाँ -
प्रतिक्रिया - विशेषता की उपस्थिति / अनुपस्थिति।
प्रीडिक्टर - न्यूमेरिक वैरिएबल प्रत्येक केस के लिए मनाया जाता है
$ {\ beta = 0 \ Rightarrow} $ P (उपस्थिति) x के प्रत्येक स्तर पर समान है।
$ {\ beta \ gt 0 \ Rightarrow} $ P (उपस्थिति) x के बढ़ने पर बढ़ता है
$ {\ beta = 0 \ Rightarrow} $ P (उपस्थिति) x के बढ़ने के साथ घटता जाता है।
उदाहरण
Problem Statement:
माइग्रेन के लिए निम्नलिखित समस्या रिज़ेटट्रिप्टन के लॉजिस्टिक रिग्रेशन को हल करें
प्रतिक्रिया - 2 घंटे में पूर्ण दर्द से राहत (हाँ / नहीं)।
प्रिडिक्टर - खुराक (मिलीग्राम): प्लेसबो (0), 2.5,5,10
| खुराक | #Patients | #राहत मिली | %राहत मिली |
|---|---|---|---|
| 0 | 67 | 2 | 3.0 |
| 2.5 | 75 | 7 | 9.3 |
| 5 | 130 | 29 | 22.3 |
| 10 | 145 | 40 | 27.6 |
Solution:
$ {\ Alpha = -2.490} और $ {\ Beta = .165} होने के बाद, हम डेटा का अनुसरण कर रहे हैं:
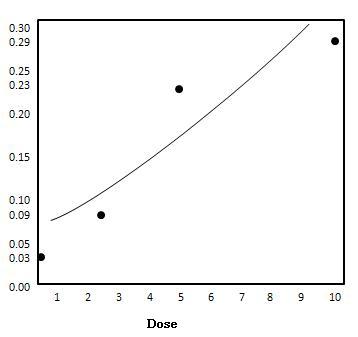
| खुराक ($ {x} $) | $ {\ Pi (x)} $ |
|---|---|
| 0 | 0.03 |
| 2.5 | 0.09 |
| 5 | 0.23 |
| 10 | 0.29 |