सांख्यिकी - वेन आरेख
वेन आरेख संस्थाओं या वस्तुओं के समूहों के बीच संबंध को दर्शाने का एक तरीका है। वेन आरेख मंडलियों से युक्त होते हैं जहाँ प्रत्येक वृत्त एक पूरे समूह का प्रतिनिधित्व करता है। वेन आरेख में असीमित वृत्त हो सकते हैं लेकिन आम तौर पर दो या तीन मंडलियों को प्राथमिकता दी जाती है अन्यथा आरेख बहुत जटिल हो जाता है।
एक वेन आरेख आकर्षित करने के लिए कदम
लोगों के निम्नलिखित सेटों पर विचार करें:
Cricket Players - $ C = \ {राम, श्याम, मोहन, रोहन, रमेश, सुरेश \ _ $
Hockey Players - $ H = \ {रमेश, नरेश, महेश, लीला, सुनीता \} $
चरण 1: एक आयत बनाएं और इसे खिलाड़ियों के रूप में लेबल करें।
चरण 2: दो मंडलियां बनाएं और उन्हें क्रिकेट और हॉकी के रूप में लेबल करें। सुनिश्चित करें कि मंडलियां एक दूसरे को ओवरलैप कर रही हैं।
चरण 3: सर्कल के अंदर नाम को प्रासंगिक के रूप में लिखें। आम नाम (ओं) को सामान्य क्षेत्र में आना चाहिए।
संघ
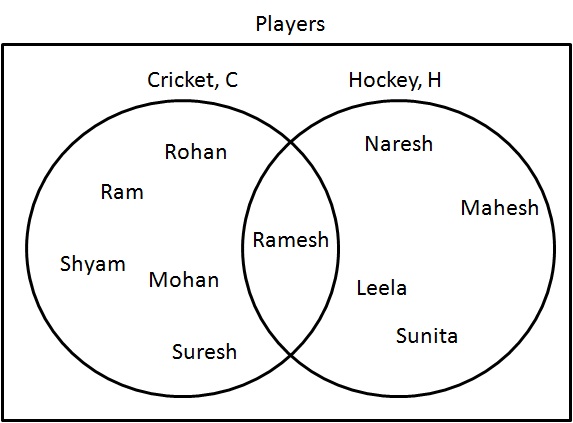
संघ ($ $ कप) एक सेट का प्रतिनिधित्व करता है जहां आइटम सभी श्रेणियों में मौजूद हैं लेकिन दोहराया नहीं जाता है।
उदाहरण
Problem Statement:
$ C \ cup H $ का वेन आरेख बनाएं।
Solution:
चरण 1: उन खिलाड़ियों को निर्धारित करें जो या तो क्रिकेट या हॉकी खेल रहे हैं। निम्नलिखित के रूप में उन्हें ड्रा करें:
$ C \ _ कप H = \ {राम, श्याम, मोहन, रोहन, रमेश, सुरेश, नरेश, महेश, लीला, सुनीता \ _ $।

चौराहा
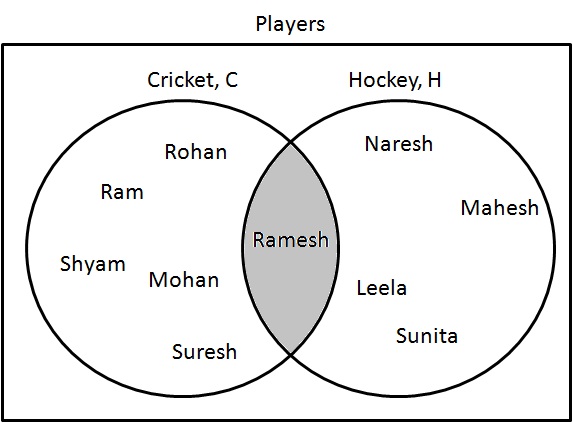
अंतर्ग्रहण ($ \ cap $) एक सेट का प्रतिनिधित्व करता है जहां आइटम दोनों श्रेणियों में मौजूद हैं।
उदाहरण
Problem Statement:
$ C \ cap H $ का वेन आरेख बनाएं।
Solution:
चरण 1: उन खिलाड़ियों को निर्धारित करें जो क्रिकेट और हॉकी दोनों खेल रहे हैं। निम्नलिखित के रूप में उन्हें ड्रा करें:
$ C \ cap H = \ {रमेश \} $।
अंतर
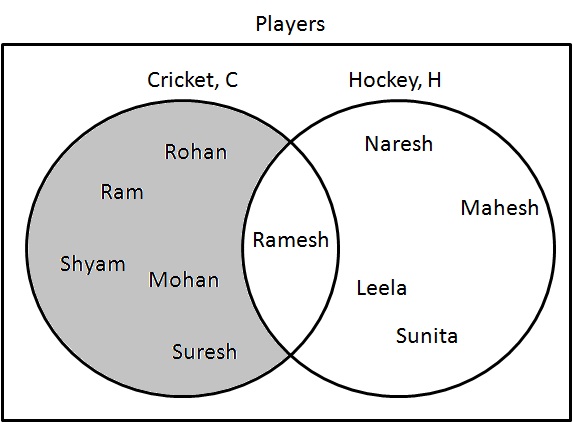
अंतर ($ - $) एक सेट का प्रतिनिधित्व करता है जहां आइटम केवल एक श्रेणी में मौजूद होते हैं और दूसरे में नहीं।
उदाहरण
Problem Statement:
$ C - H $ का वेन आरेख बनाएं।
Solution:
चरण 1: उन खिलाड़ियों को निर्धारित करें जो केवल क्रिकेट खेल रहे हैं। निम्नलिखित के रूप में उन्हें ड्रा करें:
$ C - H = \ {राम, श्याम, मोहन, रोहन, सुरेश \ _ $।