Pemrosesan Sinyal Digital - Panduan Cepat

Definisi

Segala sesuatu yang membawa informasi dapat disebut sebagai sinyal. Ini juga dapat didefinisikan sebagai kuantitas fisik yang bervariasi dengan waktu, suhu, tekanan atau dengan variabel independen seperti sinyal ucapan atau sinyal video.

Proses operasi di mana karakteristik sinyal (Amplitudo, bentuk, fasa, frekuensi, dll.) Mengalami perubahan yang dikenal sebagai pemrosesan sinyal.

Note- Sinyal yang tidak diinginkan yang mengganggu sinyal utama disebut sebagai noise. Jadi, noise juga merupakan sinyal tetapi tidak diinginkan.

Menurut representasi dan pemrosesannya, sinyal dapat diklasifikasikan ke dalam berbagai kategori yang detailnya dibahas di bawah ini.

Sinyal Waktu Berkelanjutan

Sinyal waktu kontinu didefinisikan sepanjang kontinum waktu dan dengan demikian, diwakili oleh variabel independen kontinu. Sinyal waktu kontinu sering disebut sebagai sinyal analog.

Jenis sinyal ini menunjukkan kontinuitas baik dalam amplitudo maupun waktu. Ini akan memiliki nilai setiap saat. Fungsi sinus dan cosinus adalah contoh terbaik dari sinyal waktu kontinu.

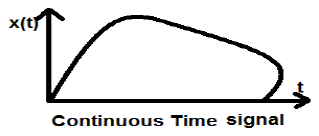
Sinyal yang ditunjukkan di atas adalah contoh sinyal waktu kontinu karena kita bisa mendapatkan nilai sinyal setiap saat.

Sinyal Waktu Diskrit

Sinyal, yang ditentukan pada waktu diskrit dikenal sebagai sinyal diskrit. Oleh karena itu, setiap variabel independen memiliki nilai yang berbeda-beda. Jadi, mereka direpresentasikan sebagai urutan angka.

Meskipun sinyal ucapan dan video memiliki hak istimewa untuk ditampilkan dalam format waktu kontinu dan diskrit; dalam keadaan tertentu, keduanya identik. Amplitudo juga menunjukkan karakteristik diskrit. Contoh sempurna dari ini adalah sinyal digital; yang amplitudo dan waktu keduanya terpisah.

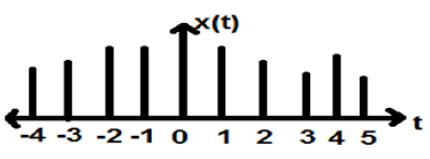
Gambar di atas menggambarkan karakteristik amplitudo diskrit sinyal diskrit selama periode waktu tertentu. Secara matematis, jenis sinyal ini dapat dirumuskan sebagai;

$$x = \left \{ x\left [ n \right ] \right \},\quad -\infty < n< \infty$$

Dimana, n adalah bilangan bulat.

Ini adalah urutan angka x, di mana n ^th nomor dalam urutan direpresentasikan sebagai x [n].

Untuk menguji suatu sistem, umumnya digunakan sinyal standar atau dasar. Sinyal ini adalah blok bangunan dasar untuk banyak sinyal kompleks. Oleh karena itu, mereka memainkan peran yang sangat penting dalam mempelajari sinyal dan sistem.

Fungsi Impuls Unit atau Delta

Sinyal yang memenuhi syarat, $\delta(t) = \lim_{\epsilon \to \infty} x(t)$dikenal sebagai sinyal impuls unit. Sinyal ini cenderung tak terhingga bila t = 0 dan cenderung nol bila t ≠ 0 sehingga daerah di bawah kurva selalu sama dengan satu. Fungsi delta memiliki amplitudo nol di mana-mana excunit_impulse.jpgept pada t = 0.

Properti Sinyal Impuls Unit

δ (t) adalah sinyal genap.
δ (t) adalah contoh sinyal energi atau daya (NENP).
Area sinyal impuls unit dapat ditulis sebagai;
Berat atau kekuatan sinyal dapat ditulis sebagai;
Area sinyal impuls tertimbang dapat ditulis sebagai -

Sinyal Langkah Satuan

Sinyal, yang memenuhi dua kondisi berikut -

$U(t) = 1(when\quad t \geq 0 )and$
$U(t) = 0 (when\quad t < 0 )$

dikenal sebagai sinyal langkah unit.

Ini memiliki sifat menunjukkan diskontinuitas pada t = 0. Pada titik diskontinuitas, nilai sinyal diberikan oleh rata-rata nilai sinyal. Sinyal ini telah diambil sebelum dan setelah titik diskontinuitas (menurut Fenomena Gibb).

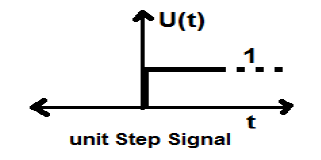
Jika kita menambahkan sinyal langkah ke sinyal langkah lain yaitu skala waktu, maka hasilnya akan menjadi satu. Ini adalah sinyal tipe daya dan nilai daya 0,5. Nilai RMS (Root mean square) adalah 0,707 dan nilai rata-ratanya juga 0,5

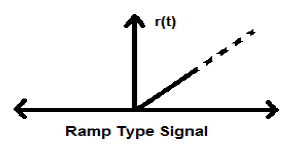
Sinyal Ramp

Integrasi hasil sinyal langkah dalam sinyal Ramp. Itu diwakili oleh r (t). Sinyal ramp juga memenuhi kondisi tersebut$r(t) = \int_{-\infty}^{t} U(t)dt = tU(t)$. Ini bukan sinyal tipe energi atau daya (NENP).

Sinyal Parabola

Integrasi sinyal Ramp mengarah ke sinyal parabola. Itu diwakili oleh p (t). Sinyal parabola juga memenuhi kondisinya$p(t) = \int_{-\infty}^{t} r(t)dt = (t^{2}/2)U(t)$. Ini bukan sinyal tipe energi atau daya (NENP).

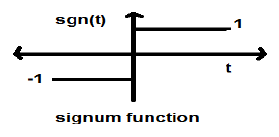
Fungsi Signum

Fungsi ini direpresentasikan sebagai

$$sgn(t) = \begin{cases}1 & for\quad t >0\\-1 & for\quad t<0\end{cases}$$

Ini adalah sinyal tipe daya. Nilai daya dan nilai RMS (Root mean square) keduanya adalah 1. Nilai rata-rata dari fungsi signum adalah nol.

Fungsi Sinc

Ini juga merupakan fungsi sinus dan ditulis sebagai -

$$SinC(t) = \frac{Sin\Pi t}{\Pi T} = Sa(\Pi t)$$

Sifat fungsi Sinc

Ini adalah sinyal tipe energi.
$Sinc(0) = \lim_{t \to 0}\frac{\sin \Pi t}{\Pi t} = 1$
$Sinc(\infty) = \lim_{t \to \infty}\frac{\sin \Pi \infty}{\Pi \infty} = 0$ (Rentang sinπ∞ bervariasi antara -1 hingga +1 tetapi apa pun yang dibagi tak terhingga sama dengan nol)
Jika $ \sin c(t) = 0 => \sin \Pi t = 0$

$\Rightarrow \Pi t = n\Pi$

$\Rightarrow t = n (n \neq 0)$

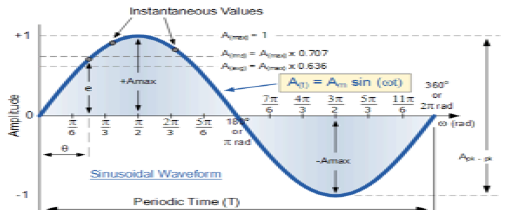
Sinyal Sinusoidal

Sinyal, yang sifatnya kontinu dikenal sebagai sinyal kontinu. Format umum dari sinyal sinusoidal adalah

$$x(t) = A\sin (\omega t + \phi )$$

Sini,

A = amplitudo sinyal

ω = Frekuensi sudut sinyal (Diukur dalam radian)

φ = Sudut fase sinyal (Diukur dalam radian)

Kecenderungan sinyal ini adalah berulang setelah periode waktu tertentu, sehingga disebut sinyal periodik. Jangka waktu sinyal diberikan sebagai;

$$T = \frac{2\pi }{\omega }$$

Tampilan diagram dari sinyal sinusoidal ditunjukkan di bawah ini.

Fungsi Persegi Panjang

Suatu sinyal dikatakan jenis fungsi persegi panjang jika memenuhi kondisi berikut -

$$\pi(\frac{t}{\tau}) = \begin{cases}1, & for\quad t\leq \frac{\tau}{2}\\0, & Otherwise\end{cases}$$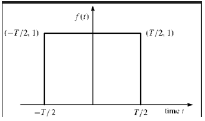

Menjadi simetris tentang sumbu Y, sinyal ini disebut sebagai sinyal genap.

Sinyal Pulsa Segitiga

Sinyal apapun, yang memenuhi kondisi berikut, dikenal sebagai sinyal segitiga.

$$\Delta(\frac{t}{\tau}) = \begin{cases}1-(\frac{2|t|}{\tau}) & for|t|<\frac{\tau}{2}\\0 & for|t|>\frac{\tau}{2}\end{cases}$$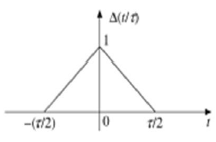

Sinyal ini simetris dengan sumbu Y. Oleh karena itu, ini juga disebut sebagai sinyal genap.

Kita telah melihat bagaimana sinyal dasar dapat direpresentasikan dalam domain waktu kontinu. Mari kita lihat bagaimana sinyal dasar dapat direpresentasikan dalam Domain Waktu Diskrit.

Urutan Impuls Unit

Ini dilambangkan sebagai δ (n) dalam domain waktu diskrit dan dapat didefinisikan sebagai;

$$\delta(n)=\begin{cases}1, & for \quad n=0\\0, & Otherwise\end{cases}$$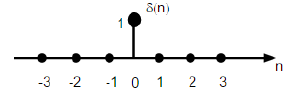

Sinyal Langkah Satuan

Sinyal langkah satuan waktu diskrit didefinisikan sebagai;

$$U(n)=\begin{cases}1, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$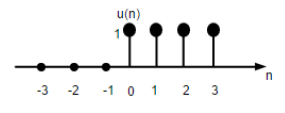

Gambar di atas menunjukkan representasi grafis dari fungsi langkah diskrit.

Fungsi Ramp Unit

Fungsi ramp unit diskrit dapat didefinisikan sebagai -

$$r(n)=\begin{cases}n, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$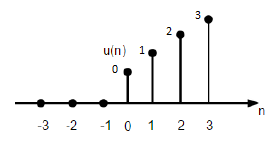

Gambar yang diberikan di atas menunjukkan representasi grafis dari sinyal ramp diskrit.

Fungsi Parabola

Fungsi parabola unit diskrit dilambangkan sebagai p (n) dan dapat didefinisikan sebagai;

$$p(n) = \begin{cases}\frac{n^{2}}{2} ,& for \quad n\geq0\\0, & for \quad n<0\end{cases}$$

Dalam istilah fungsi unit step dapat ditulis sebagai;

$$P(n) = \frac{n^{2}}{2}U(n)$$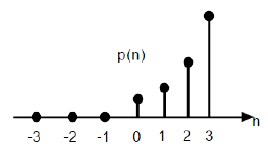

Gambar yang diberikan di atas menunjukkan representasi grafis dari urutan parabola.

Sinyal Sinusoidal

Semua sinyal waktu kontinu bersifat periodik. Urutan sinusoidal waktu-diskrit mungkin atau mungkin tidak periodik. Mereka bergantung pada nilai ω. Agar sinyal waktu diskrit menjadi periodik, frekuensi sudut ω harus merupakan kelipatan rasional 2π.

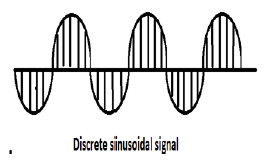
Sinyal sinusoidal diskrit ditunjukkan pada gambar di atas.

Bentuk diskrit dari sinyal sinusoidal dapat direpresentasikan dalam format -

$$x(n) = A\sin(\omega n + \phi)$$

Di sini A, ω dan φ memiliki arti yang biasa dan n adalah bilangan bulat. Periode waktu sinyal sinusoidal diskrit diberikan oleh -

$$N =\frac{2\pi m}{\omega}$$

Dimana, N dan m adalah bilangan bulat.

Sinyal waktu kontinu dapat diklasifikasikan menurut kondisi atau operasi berbeda yang dilakukan pada sinyal.

Sinyal Genap dan Ganjil

Bahkan Signal

Suatu sinyal dikatakan bahkan jika memenuhi kondisi berikut;

$$x(-t) = x(t)$$

Pembalikan waktu sinyal tidak menyiratkan perubahan amplitudo apa pun di sini. Misalnya, perhatikan gelombang segitiga yang ditunjukkan di bawah ini.

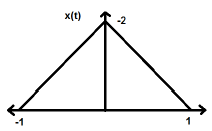
Sinyal segitiga adalah sinyal genap. Karena, ini simetris tentang sumbu Y. Kita dapat mengatakan itu adalah bayangan cermin tentang sumbu Y.

Perhatikan sinyal lain seperti yang ditunjukkan pada gambar di bawah ini.

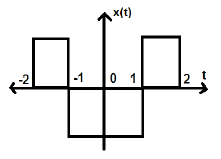
Kita dapat melihat bahwa sinyal di atas sama simetris dengan sumbu Y.

Sinyal Ganjil

Suatu sinyal dikatakan ganjil, jika memenuhi kondisi berikut

$$x(-t) = -x(t)$$

Di sini, baik pembalikan waktu dan perubahan amplitudo terjadi secara bersamaan.

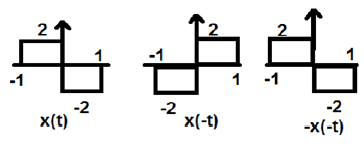
Pada gambar di atas, kita bisa melihat sinyal langkah x (t). Untuk menguji apakah sinyal tersebut ganjil atau tidak, pertama kita lakukan pembalikan waktu yaitu x (-t) dan hasilnya seperti yang terlihat pada gambar. Kemudian kita membalik amplitudo dari sinyal yang dihasilkan yaitu –x (-t) dan kita mendapatkan hasil seperti yang ditunjukkan pada gambar.

Jika kita membandingkan bentuk gelombang pertama dan ketiga, kita dapat melihat bahwa keduanya sama, yaitu x (t) = -x (-t), yang memenuhi kriteria kita. Oleh karena itu, sinyal di atas merupakan sinyal Ganjil.

Beberapa hasil penting yang terkait dengan sinyal genap dan ganjil diberikan di bawah ini.

Genap × Genap = Genap
Ganjil × Ganjil = Genap
Genap × Ganjil = Ganjil
Genap ± Genap = Genap
Ganjil ± Ganjil = Ganjil
Genap ± Ganjil = Tidak genap maupun ganjil

Representasi sinyal apa pun ke dalam bentuk genap atau ganjil

Beberapa sinyal tidak dapat langsung diklasifikasikan ke dalam tipe genap atau ganjil. Ini direpresentasikan sebagai kombinasi dari sinyal genap dan ganjil.

$$x(t)\rightarrow x_{e}(t)+x_{0}(t)$$

Dimana x _e (t) mewakili sinyal genap dan x _o (t) mewakili sinyal ganjil

$$x_{e}(t)=\frac{[x(t)+x(-t)]}{2}$$

Dan

$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$

Contoh

Temukan bagian sinyal yang genap dan ganjil $x(n) = t+t^{2}+t^{3}$

Solution - Dari membalikkan x (n), kita dapatkan

$$x(-n) = -t+t^{2}-t^{3}$$

Sekarang, menurut rumus, bagian genap

$$x_{e}(t) = \frac{x(t)+x(-t)}{2}$$

$$= \frac{[(t+t^{2}+t^{3})+(-t+t^{2}-t^{3})]}{2}$$

$$= t^{2}$$

Demikian pula menurut rumus bagian ganjil adalah

$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$

$$= \frac{[(t+t^{2}+t^{3})-(-t+t^{2}-t^{3})]}{2}$$

$$= t+t^{3}$$

Sinyal Berkala dan Non Berkala

Sinyal Berkala

Sinyal periodik berulang setelah interval waktu tertentu. Kami dapat menunjukkan ini dalam bentuk persamaan sebagai -

$$x(t) = x(t)\pm nT$$

Dimana, n = bilangan bulat (1,2,3 ……)

T = Periode waktu fundamental (FTP) ≠ 0 dan ≠ ∞

Periode waktu fundamental (FTP) adalah nilai waktu positif dan tetap terkecil yang sinyalnya bersifat periodik.

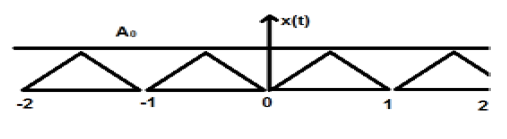
Sinyal segitiga ditunjukkan pada gambar di atas amplitudo A. Di sini, sinyal diulang setiap 1 detik. Oleh karena itu, kita dapat mengatakan bahwa sinyalnya bersifat periodik dan FTP-nya adalah 1 detik.

Sinyal Non-Berkala

Sederhananya, kita dapat mengatakan, sinyal, yang tidak periodik bersifat non-periodik. Jelasnya, sinyal ini tidak akan terulang kembali setelah waktu jeda.

Sinyal non-periodik tidak mengikuti format tertentu; oleh karena itu, tidak ada persamaan matematika tertentu yang dapat mendeskripsikannya.

Sinyal Energi dan Daya

Suatu sinyal dikatakan sebagai sinyal Energi, jika dan hanya jika, energi total yang terkandung terbatas dan bukan nol (0 <E <∞). Oleh karena itu, untuk sinyal jenis energi apa pun, total sinyal yang dinormalisasi adalah terbatas dan bukan nol.

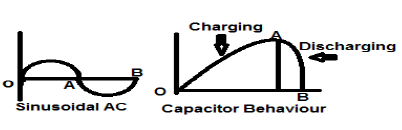
Sinyal arus AC sinusoidal adalah contoh sempurna dari sinyal tipe Energi karena dalam setengah siklus positif dalam satu kasus dan kemudian negatif dalam setengah siklus berikutnya. Oleh karena itu, daya rata-ratanya menjadi nol.

Kapasitor lossless juga merupakan contoh sempurna dari sinyal tipe Energi karena ketika dihubungkan ke sumber, ia mengisi hingga tingkat optimal dan ketika sumber dilepas, ia menghilangkan jumlah energi yang sama melalui beban dan membuat daya rata-ratanya menjadi nol.

Untuk setiap sinyal hingga x (t) energi dapat disimbolkan sebagai E dan ditulis sebagai;

$$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$

Densitas spektral sinyal jenis energi memberikan jumlah energi yang didistribusikan pada berbagai tingkat frekuensi.

Sinyal tipe daya

Suatu sinyal dikatakan sebagai sinyal tipe daya, jika dan hanya jika, daya rata-rata yang dinormalisasi adalah terbatas dan bukan nol yaitu (0 <p <∞). Untuk sinyal tipe daya, daya rata-rata yang dinormalisasi terbatas dan bukan nol. Hampir semua sinyal periodik adalah sinyal daya dan daya rata-ratanya terbatas dan bukan nol.

Dalam bentuk matematis, kekuatan sinyal x (t) dapat ditulis sebagai;

$$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$

Perbedaan antara Energi dan Sinyal Daya

Tabel berikut merangkum perbedaan Sinyal Energi dan Daya.

Sinyal daya	Sinyal Energi
Sinyal periodik praktis adalah sinyal daya.	Sinyal non-periodik adalah sinyal energi.
Di sini, daya rata-rata yang dinormalkan terbatas dan bukan nol.	Di sini, total energi yang dinormalisasi adalah berhingga dan bukan nol.
Secara matematis, $$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$	Secara matematis, $$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$
Keberadaan sinyal ini tidak terbatas dari waktu ke waktu.	Sinyal ini ada untuk jangka waktu terbatas.
Energi sinyal daya tidak terbatas selama waktu yang tidak terbatas.	Kekuatan sinyal energi adalah nol selama waktu yang tak terbatas.

Contoh Terpecahkan

Example 1 - Temukan Kekuatan sinyal $z(t) = 2\cos(3\Pi t+30^{o})+4\sin(3\Pi +30^{o})$

Solution- Kedua sinyal di atas ortogonal satu sama lain karena istilah frekuensinya identik satu sama lain juga memiliki perbedaan fasa yang sama. Jadi, kekuatan total akan menjadi penjumlahan dari kekuatan individu.

Membiarkan $z(t) = x(t)+y(t)$

Dimana $x(t) = 2\cos (3\Pi t+30^{o})$ dan $y(t) = 4\sin(3\Pi +30^{o})$

Kekuatan dari $x(t) = \frac{2^{2}}{2} = 2$

Kekuatan dari $y(t) = \frac{4^{2}}{2} = 8$

Karena itu, $P(z) = p(x)+p(y) = 2+8 = 10$… Ans.

Example 2 - Uji apakah sinyal diberikan $x(t) = t^{2}+j\sin t$ konjugasi atau tidak?

Solution- Di sini, bagian nyata yang t ² adalah bagian genap dan ganjil (imajiner)$\sin t$aneh. Jadi sinyal di atas adalah sinyal Konjugasi.

Example 3 - Verifikasi apakah $X(t)= \sin \omega t$ adalah sinyal ganjil atau sinyal genap.

Solution - Diberikan $X(t) = \sin \omega t$

Dengan pembalikan waktu, kita akan mendapatkan $\sin (-\omega t)$

Tapi kami tahu itu $\sin(-\phi) = -\sin \phi$.

Karena itu,

$$\sin (-\omega t) = -\sin \omega t$$

Ini memenuhi kondisi sinyal menjadi ganjil. Karena itu,$\sin \omega t$ adalah sinyal yang aneh.

Sama seperti sinyal waktu kontinu, sinyal waktu diskrit dapat diklasifikasikan menurut kondisi atau operasi sinyal.

Sinyal Genap dan Ganjil

Bahkan Signal

Suatu sinyal dikatakan genap atau simetris jika memenuhi kondisi berikut;

$$x(-n) = x(n)$$

Di sini, kita dapat melihat bahwa x (-1) = x (1), x (-2) = x (2) dan x (-n) = x (n). Jadi, ini adalah sinyal genap.

Sinyal Ganjil

Suatu sinyal dikatakan ganjil jika memenuhi kondisi berikut;

$$x(-n) = -x(n)$$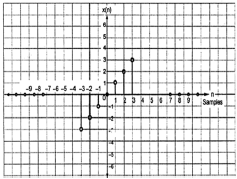

Dari gambar tersebut, kita dapat melihat bahwa x (1) = -x (-1), x (2) = -x (2) dan x (n) = -x (-n). Oleh karena itu, ini adalah sinyal ganjil dan juga anti-simetris.

Sinyal Berkala dan Non Berkala

Sinyal waktu diskrit bersifat periodik jika dan hanya jika memenuhi kondisi berikut -

$$x(n+N) = x(n)$$

Di sini, sinyal x (n) berulang sendiri setelah periode N. Hal ini paling baik dipahami dengan mempertimbangkan sinyal kosinus -

$$x(n) = A \cos(2\pi f_{0}n+\theta)$$ $$x(n+N) = A\cos(2\pi f_{0}(n+N)+\theta) = A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$ $$= A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$

Agar sinyal menjadi periodik, kondisi berikut harus dipenuhi;

$$x(n+N) = x(n)$$ $$\Rightarrow A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta) = A \cos(2\pi f_{0}n+\theta)$$

yaitu $2\pi f_{0}N$ adalah kelipatan integral dari $2\pi$

$$2\pi f_{0}N = 2\pi K$$ $$\Rightarrow N = \frac{K}{f_{0}}$$

Frekuensi sinyal sinusoidal diskrit dipisahkan oleh kelipatan integral $2\pi$.

Sinyal Energi dan Daya

Sinyal Energi

Energi sinyal waktu diskrit dilambangkan sebagai E. Secara matematis, ini dapat ditulis sebagai;

$$E = \displaystyle \sum\limits_{n=-\infty}^{+\infty}|x(n)|^2$$

Jika masing-masing individu menghargai $x(n)$dikuadratkan dan ditambahkan, kita mendapatkan sinyal energi. Sini$x(n)$ adalah sinyal energi dan energinya terbatas dari waktu ke waktu yaitu $ 0 <E <\ infty $

Sinyal Daya

Daya rata-rata dari sinyal diskrit direpresentasikan sebagai P. Secara matematis, ini dapat ditulis sebagai;

$$P = \lim_{N \to \infty} \frac{1}{2N+1}\displaystyle\sum\limits_{n=-N}^{+N} |x(n)|^2$$

Di sini, daya terbatas yaitu 0 <P <∞. Namun, ada beberapa sinyal, yang bukan milik energi atau sinyal tipe daya.

Ada sinyal lain, yang merupakan hasil operasi yang dilakukan padanya. Beberapa jenis sinyal yang umum dibahas di bawah ini.

Sinyal Konjugasi

Sinyal yang memenuhi kondisi tersebut $x(t) = x*(-t)$ disebut sinyal konjugasi.

Membiarkan $x(t) = a(t)+jb(t)$... eqn. 1

Begitu, $x(-t) = a(-t)+jb(-t)$

Dan $x*(-t) = a(-t)-jb(-t)$... eqn. 2

Menurut Kondisi, $x(t) = x*(-t)$

Jika kita membandingkan persamaan turunan 1 dan 2, kita dapat melihat bahwa bagian sebenarnya genap, sedangkan bagian imajinernya ganjil. Ini adalah kondisi sinyal menjadi tipe konjugasi.

Konjugasi Sinyal Anti-Simetris

Sinyal, yang memenuhi kondisi tersebut $x(t) = -x*(-t)$ disebut sinyal anti-simetris konjugasi

Membiarkan $x(t) = a(t)+jb(t)$... eqn. 1

Begitu $x(-t) = a(-t)+jb(-t)$

Dan $x*(-t) = a(-t)-jb(-t)$

$-x*(-t) = -a(-t)+jb(-t)$... eqn. 2

Menurut Kondisi $x(t) = -x*(-t)$

Sekarang, bandingkan lagi, kedua persamaan seperti yang kita lakukan untuk sinyal konjugasi. Di sini, kita akan menemukan bahwa bagian yang sebenarnya adalah ganjil dan bagian imajinernya adalah genap. Ini adalah kondisi sinyal menjadi tipe anti-simetris konjugasi.

Contoh

Biarkan sinyal yang diberikan $x(t) = \sin t+jt^{2}$.

Di sini, makhluk yang sebenarnya $\sin t$ aneh dan bagian imajiner $t^2$adalah genap. Jadi, sinyal ini dapat diklasifikasikan sebagai sinyal anti-simetris konjugasi.

Fungsi apa pun dapat dibagi menjadi dua bagian. Satu bagian menjadi konjugasi simetri dan bagian lainnya anti simetris konjugasi. Jadi setiap sinyal x (t) dapat ditulis sebagai

$$x(t) = xcs(t)+xcas(t)$$

Dimana $xcs(t)$ adalah sinyal simetris konjugasi dan $xcas(t)$ adalah sinyal anti simetris konjugasi

$$xcs(t) = \frac{[x(t)+x*(-t)]}{2}$$

Dan

$$xcas(t) = \frac{[x(t)-x*(-t)]}{2}$$

Sinyal Simetris Setengah Gelombang

Ketika sinyal memenuhi kondisi tersebut $cx(t) = -x(t\pm (\frac{T_{0}}{2}))$, ini disebut sinyal simetris setengah gelombang. Di sini, pembalikan amplitudo dan pergeseran waktu sinyal berlangsung setengah waktu. Untuk sinyal simetris setengah gelombang, nilai rata-rata akan menjadi nol tetapi tidak demikian halnya ketika situasinya terbalik.

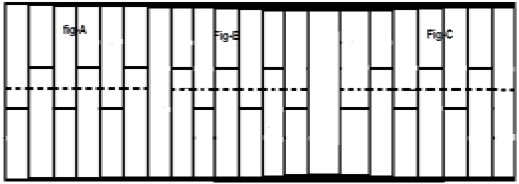
Pertimbangkan sinyal x (t) seperti yang ditunjukkan pada gambar A di atas. Langkah pertama adalah mengubah waktu sinyal dan membuatnya$x[t-(\frac{T}{2})]$. Jadi, sinyal baru diubah seperti yang ditunjukkan pada gambar B. Selanjutnya, kami membalikkan amplitudo sinyal, yaitu membuatnya$-x[t-(\frac{T}{2})]$ seperti yang ditunjukkan pada gambar C. Karena, sinyal ini berulang sendiri setelah pergeseran paruh waktu dan pembalikan amplitudo, ini adalah sinyal simetris setengah gelombang.

Sinyal Ortogonal

Dua sinyal x (t) dan y (t) dikatakan ortogonal jika memenuhi dua kondisi berikut.

Condition 1 - $\int_{-\infty}^{\infty}x(t)y(t) = 0$ [untuk sinyal non-periodik]

Condition 2 - $\int x(t)y(t) = 0$ [Untuk Sinyal berkala]

Sinyal, yang mengandung harmonik ganjil (3 ^rd , 5 ^th , 7 ^th ... dll.) Dan memiliki frekuensi yang berbeda, saling ortogonal satu sama lain.

Dalam sinyal tipe trigonometri, fungsi sinus dan fungsi kosinus juga ortogonal satu sama lain; asalkan, mereka memiliki frekuensi yang sama dan berada dalam fase yang sama. Dengan cara yang sama DC (sinyal arus searah) dan sinyal sinusoidal juga ortogonal satu sama lain. Jika x (t) dan y (t) adalah dua sinyal ortogonal dan$z(t) = x(t)+y(t)$ maka kekuatan dan energi z (t) dapat ditulis sebagai;

$$P(z) = p(x)+p(y)$$ $$E(z) = E(x)+E(y)$$

Contoh

Analisis sinyalnya: $z(t) = 3+4\sin(2\pi t+30^0)$

Di sini, sinyal terdiri dari sinyal DC (3) dan satu fungsi sinus. Jadi, menurut properti sinyal ini adalah sinyal ortogonal dan dua sub-sinyal di dalamnya saling ortogonal satu sama lain.

Pergeseran berarti pergerakan sinyal, baik dalam domain waktu (di sekitar sumbu Y) maupun dalam domain amplitudo (di sekitar sumbu X). Dengan demikian, kita dapat mengklasifikasikan pergeseran ke dalam dua kategori yang dinamakan sebagai Pergeseran waktu dan Pergeseran amplitudo, ini selanjutnya dibahas di bawah.

Pergeseran Waktu

Pergeseran waktu berarti pergeseran sinyal dalam domain waktu. Secara matematis, dapat ditulis sebagai

$$x(t) \rightarrow y(t+k)$$

Nilai K ini bisa positif atau bisa negatif. Menurut tanda nilai k, ada dua jenis perpindahan gigi yang disebut dengan perpindahan kanan dan perpindahan kiri.

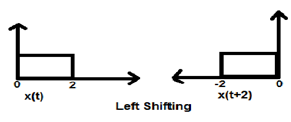
Kasus 1 (K> 0)

Ketika K lebih besar dari nol, pergeseran sinyal terjadi ke arah "kiri" dalam domain waktu. Karenanya, jenis perpindahan ini dikenal sebagai Pergeseran Kiri sinyal.

Example

Kasus 2 (K <0)

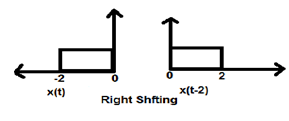
Ketika K kurang dari nol, pergeseran sinyal terjadi ke arah kanan dalam domain waktu. Oleh karena itu, jenis perpindahan ini disebut dengan perpindahan kanan.

Example

Gambar yang diberikan di bawah ini menunjukkan pergeseran kanan sinyal sebesar 2.

Pergeseran Amplitudo

Pergeseran amplitudo berarti pergeseran sinyal dalam domain amplitudo (di sekitar sumbu X). Secara matematis, ini dapat direpresentasikan sebagai -

$$x(t) \rightarrow x(t)+K$$

Nilai K ini bisa positif atau negatif. Karenanya, kami memiliki dua jenis pergeseran amplitudo yang selanjutnya dibahas di bawah ini.

Kasus 1 (K> 0)

Ketika K lebih besar dari nol, pergeseran sinyal terjadi ke arah atas pada sumbu x. Oleh karena itu, jenis perpindahan ini disebut dengan perpindahan ke atas.

Example

Mari kita pertimbangkan sinyal x (t) yang diberikan sebagai;

$$x = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$

Mari kita ambil K = + 1 sehingga sinyal baru dapat ditulis sebagai -

$y(t) \rightarrow x(t)+1$ Jadi, y (t) akhirnya bisa ditulis sebagai;

$$x(t) = \begin{cases}1, & t < 0\\2, & 0\leq t\leq 2\\ 1, & t>0\end{cases}$$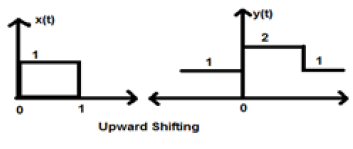

Kasus 2 (K <0)

Ketika K kurang dari nol, pergeseran sinyal terjadi ke arah bawah pada sumbu X. Oleh karena itu, ini disebut pergeseran sinyal ke bawah.

Example

Mari kita pertimbangkan sinyal x (t) yang diberikan sebagai;

$$x(t) = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$

Mari kita ambil K = -1 sehingga sinyal baru dapat ditulis sebagai;

$y(t)\rightarrow x(t)-1$ Jadi, y (t) akhirnya bisa ditulis sebagai;

$$y(t) = \begin{cases}-1, & t < 0\\0, & 0\leq t\leq 2\\ -1, & t>0\end{cases}$$

Penskalaan sinyal berarti, konstanta dikalikan dengan waktu atau amplitudo sinyal.

Penskalaan Waktu

Jika sebuah konstanta dikalikan dengan sumbu waktu maka itu dikenal sebagai Skala waktu. Ini secara matematis dapat direpresentasikan sebagai;

$x(t) \rightarrow y(t) = x(\alpha t)$ atau $x(\frac{t}{\alpha})$; dimana α ≠ 0

Jadi sumbu y sama, besaran sumbu x berkurang atau bertambah sesuai dengan tanda konstanta (baik positif maupun negatif). Oleh karena itu, penskalaan juga dapat dibagi menjadi dua kategori seperti yang dibahas di bawah ini.

Kompresi Waktu

Setiap kali alpha lebih besar dari nol, amplitudo sinyal akan dibagi dengan alpha sedangkan nilai sumbu Y tetap sama. Ini dikenal sebagai Kompresi Waktu.

Example

Mari kita pertimbangkan sinyal x (t), yang ditunjukkan seperti pada gambar di bawah. Mari kita ambil nilai alpha sebagai 2. Jadi, y (t) akan menjadi x (2t), yang diilustrasikan pada gambar.

Jelasnya, kita dapat melihat dari gambar di atas bahwa besaran waktu pada sumbu y tetap sama tetapi amplitudo pada sumbu x berkurang dari 4 menjadi 2. Oleh karena itu, ini adalah kasus Kompresi Waktu.

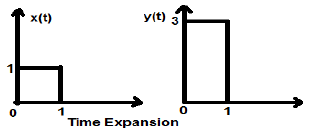
Perluasan Waktu

Ketika waktu dibagi dengan alfa konstan, besaran sumbu Y dari sinyal dikalikan kali alfa, menjaga besaran sumbu X sebagaimana adanya. Oleh karena itu, ini disebut sinyal tipe ekspansi Waktu.

Example

Mari kita pertimbangkan sinyal persegi x (t), besarnya 1. Ketika kita menskalakannya dengan konstanta 3, sedemikian rupa sehingga $x(t) \rightarrow y(t) \rightarrow x(\frac{t}{3})$, kemudian amplitudo sinyal dimodifikasi sebanyak 3 kali seperti yang ditunjukkan pada gambar di bawah ini.

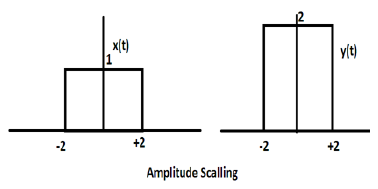
Penskalaan Amplitudo

Perkalian konstanta dengan amplitudo sinyal menyebabkan penskalaan amplitudo. Bergantung pada tanda konstanta, itu bisa berupa skala amplitudo atau atenuasi. Mari kita pertimbangkan sinyal gelombang persegi x (t) = Π (t / 4).

Misalkan kita mendefinisikan fungsi lain y (t) = 2 Π (t / 4). Dalam kasus ini, nilai sumbu y akan digandakan, dengan mempertahankan nilai sumbu waktu sebagaimana adanya. Diilustrasikan pada gambar yang diberikan di bawah ini.

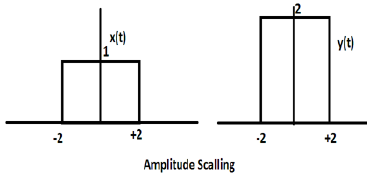
Pertimbangkan fungsi gelombang persegi lain yang didefinisikan sebagai z (t) di mana z (t) = 0,5 Π (t / 4). Di sini, amplitudo dari fungsi z (t) akan menjadi setengah dari x (t) yaitu sumbu waktu tetap sama, sumbu amplitudo akan dibelah dua. Ini diilustrasikan oleh gambar yang diberikan di bawah ini.

Setiap kali waktu dalam sinyal dikalikan dengan -1, sinyal dibalik. Ini menghasilkan bayangan cermin tentang sumbu Y atau X. Ini dikenal sebagai Pembalikan sinyal.

Pembalikan dapat diklasifikasikan menjadi dua jenis berdasarkan kondisi apakah waktu atau amplitudo sinyal dikalikan -1.

Pembalikan Waktu

Kapan pun waktu sinyal dikalikan dengan -1, itu dikenal sebagai pembalikan waktu sinyal. Dalam hal ini, sinyal menghasilkan bayangan cerminnya tentang sumbu Y. Secara matematis, ini dapat ditulis sebagai;

$$x(t) \rightarrow y(t) \rightarrow x(-t)$$

Hal ini paling baik dipahami dengan contoh berikut.

Dalam contoh di atas, kita dapat dengan jelas melihat bahwa sinyal telah terbalik tentang sumbu Y-nya. Jadi, ini adalah salah satu jenis penskalaan waktu juga, tetapi di sini kuantitas penskalaannya selalu (-1).

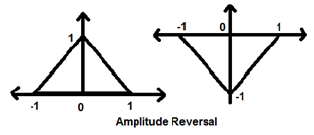
Pembalikan Amplitudo

Setiap kali amplitudo sinyal dikalikan dengan -1, maka itu dikenal sebagai pembalikan amplitudo. Dalam hal ini, sinyal menghasilkan bayangan cerminnya tentang sumbu X. Secara matematis, ini dapat ditulis sebagai;

$$x(t)\rightarrow y(t)\rightarrow -x(t)$$

Perhatikan contoh berikut. Pembalikan amplitudo dapat dilihat dengan jelas.

Dua operasi yang sangat penting dilakukan pada sinyal adalah Diferensiasi dan Integrasi.

Diferensiasi

Diferensiasi sinyal x (t) berarti representasi kemiringan sinyal tersebut terhadap waktu. Secara matematis, ini direpresentasikan sebagai;

$$x(t)\rightarrow \frac{dx(t)}{dt}$$

Dalam kasus diferensiasi OPAMP, metodologi ini sangat membantu. Kami dapat dengan mudah membedakan sinyal secara grafis daripada menggunakan rumus. Namun, syaratnya adalah bahwa sinyal harus berbentuk persegi panjang atau segitiga, yang sering terjadi.

Sinyal Asli	Sinyal Diferensiasi
Lereng	Langkah
Langkah	Impuls
Impuls	1

Tabel di atas menggambarkan kondisi sinyal setelah dibedakan. Misalnya, sinyal ramp diubah menjadi sinyal langkah setelah diferensiasi. Demikian pula, sinyal langkah satuan menjadi sinyal impuls.

Contoh

Biarlah sinyal yang diberikan kepada kita $x(t) = 4[r(t)-r(t-2)]$. Ketika sinyal ini diplot, itu akan terlihat seperti yang ada di sisi kiri gambar yang diberikan di bawah ini. Sekarang, tujuan kami adalah untuk membedakan sinyal yang diberikan.

Untuk memulainya, kita akan mulai mendiferensiasi persamaan yang diberikan. Kita tahu bahwa sinyal ramp setelah diferensiasi memberikan sinyal langkah satuan.

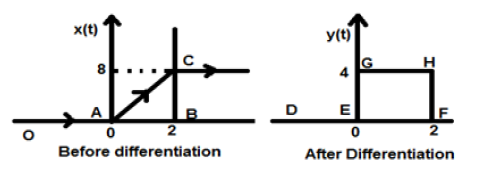
Jadi sinyal yang dihasilkan y (t) dapat ditulis sebagai;

$y(t) = \frac{dx(t)}{dt}$

$= \frac{d4[r(t)-r(t-2)]}{dt}$

$= 4[u(t)-u(t-2)]$

Sekarang sinyal ini akhirnya diplot, yang ditunjukkan di sisi kanan gambar di atas.

Integrasi sinyal apa pun berarti penjumlahan sinyal itu dalam domain waktu tertentu untuk mendapatkan sinyal yang dimodifikasi. Secara matematis, ini dapat direpresentasikan sebagai -

$$x(t)\rightarrow y(t) = \int_{-\infty}^{t}x(t)dt$$

Di sini juga, dalam sebagian besar kasus, kita dapat melakukan integrasi matematika dan menemukan sinyal yang dihasilkan, tetapi integrasi langsung dalam urutan cepat dimungkinkan untuk sinyal yang digambarkan dalam format persegi panjang secara grafis. Seperti diferensiasi, di sini juga, kami akan merujuk tabel untuk mendapatkan hasilnya dengan cepat.

Sinyal Asli	Sinyal Terintegrasi
1	impuls
Impuls	langkah
Langkah	Lereng

Contoh

Mari kita pertimbangkan sebuah sinyal $x(t) = u(t)-u(t-3)$. Itu ditunjukkan pada Gambar-1 di bawah ini. Jelas, kita dapat melihat bahwa itu adalah sinyal langkah. Sekarang kami akan mengintegrasikannya. Mengacu pada tabel, kita tahu bahwa integrasi sinyal langkah menghasilkan sinyal ramp.

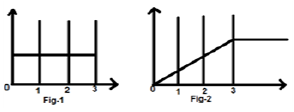
Namun, kami akan menghitungnya secara matematis,

$y(t) = \int_{-\infty}^{t}x(t)dt$

$= \int_{-\infty}^{t}[u(t)-u(t-3)]dt$

$= \int_{-\infty}^{t}u(t)dt-\int_{-\infty}^{t}u(t-3)dt$

$= r(t)-r(t-3)$

Hal yang sama diplot seperti yang ditunjukkan pada gbr-2,

Konvolusi dua sinyal dalam domain waktu setara dengan perkalian representasi mereka dalam domain frekuensi. Secara matematis, kita dapat menulis lilitan dua sinyal sebagai

$$y(t) = x_{1}(t)*x_{2}(t)$$ $$= \int_{-\infty}^{\infty}x_{1}(p).x_{2}(t-p)dp$$

Langkah-langkah untuk konvolusi

Ambil sinyal x ₁ (t) dan taruh t = p di situ sehingga menjadi x ₁ (p).
Ambil sinyal x ₂ (t) dan lakukan langkah 1 dan jadikan x ₂ (p).
Buatlah pelipatan sinyal yaitu x ₂ (-p).
Lakukan perpindahan waktu dari sinyal di atas x ₂ [- (pt)]
Kemudian lakukan perkalian kedua sinyal tersebut. yaitu$x_{1}(p).x_{2}[−(p−t)]$

Contoh

Mari kita lakukan konvolusi sinyal langkah u (t) dengan jenisnya sendiri.

$y(t) = u(t)*u(t)$

$= \int_{-\infty}^{\infty}[u(p).u[-(p-t)]dp$

Sekarang t ini bisa lebih besar dari atau kurang dari nol, yang ditunjukkan pada gambar di bawah ini

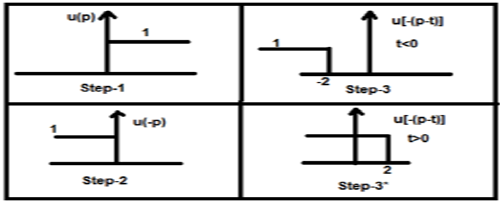
Jadi, dengan kasus di atas, hasilnya muncul dengan kemungkinan sebagai berikut

$y(t) = \begin{cases}0, & if\quad t<0\\\int_{0}^{t}1dt, & for\quad t>0\end{cases}$

$= \begin{cases}0, & if\quad t<0\\t, & t>0\end{cases} = r(t)$

Sifat Konvolusi

Komutatif

Ini menyatakan bahwa urutan konvolusi tidak masalah, yang secara matematis dapat ditunjukkan sebagai

$$x_{1}(t)*x_{2}(t) = x_{2}(t)*x_{1}(t)$$

Asosiatif

Ini menyatakan bahwa urutan konvolusi yang melibatkan tiga sinyal, dapat berupa apa saja. Secara matematis, ini dapat ditampilkan sebagai;

$$x_{1}(t)*[x_{2}(t)*x_{3}(t)] = [x_{1}(t)*x_{2}(t)]*x_{3}(t)$$

Distributif

Dua sinyal dapat ditambahkan terlebih dahulu, dan kemudian konvolusinya dapat dibuat ke sinyal ketiga. Ini setara dengan konvolusi dua sinyal secara individual dengan sinyal ketiga dan akhirnya ditambahkan. Secara matematis, ini dapat ditulis sebagai;

$$x_{1}(t)*[x_{2}(t)+x_{3}(t)] = [x_{1}(t)*x_{2}(t)+x_{1}(t)*x_{3}(t)]$$

Daerah

Jika suatu sinyal adalah hasil dari konvolusi dua sinyal maka luas sinyal tersebut adalah perkalian dari sinyal-sinyal individual tersebut. Secara matematis ini bisa ditulis

Jika $y(t) = x_{1}*x_{2}(t)$

Maka Luas y (t) = Luas x ₁ (t) X Luas x ₂ (t)

Penskalaan

Jika dua sinyal diskalakan ke beberapa konstanta "a" yang tidak diketahui dan konvolusi dilakukan, sinyal resultan juga akan dikonvolusi ke konstanta "a" yang sama dan akan dibagi dengan kuantitas tersebut seperti yang ditunjukkan di bawah ini.

Jika, $x_{1}(t)*x_{2}(t) = y(t)$

Kemudian, $x_{1}(at)*x_{2}(at) = \frac{y(at)}{a}, a \ne 0$

Menunda

Misalkan sinyal y (t) adalah hasil dari konvolusi dua sinyal x1 (t) dan x2 (t). Jika kedua sinyal masing-masing tertunda oleh waktu t1 dan t2, maka sinyal resultan y (t) akan ditunda oleh (t1 + t2). Secara matematis, dapat ditulis sebagai -

Jika, $x_{1}(t)*x_{2}(t) = y(t)$

Kemudian, $x_{1}(t-t_{1})*x_{2}(t-t_{2}) = y[t-(t_{1}+t_{2})]$

Contoh Terpecahkan

Example 1 - Tentukan konvolusi sinyal u (t-1) dan u (t-2).

Solution- Sinyal yang diberikan adalah u (t-1) dan u (t-2). Konvolusi mereka dapat dilakukan seperti yang ditunjukkan di bawah ini -

$y(t) = u(t-1)*u(t-2)$

$y(t) = \int_{-\infty}^{+\infty}[u(t-1).u(t-2)]dt$

$= r(t-1)+r(t-2)$

$= r(t-3)$

Example 2 - Temukan konvolusi dua sinyal yang diberikan oleh

$x_{1}(n) = \lbrace 3,-2, 2\rbrace $

$x_{2}(n) = \begin{cases}2, & 0\leq n\leq 4\\0, & x > elsewhere\end{cases}$

Solution -

x ₂ (n) dapat diterjemahkan sebagai$x_{2}(n) = \lbrace 2,2,2,2,2\rbrace Originalfirst$

x ₁ (n) sebelumnya diberikan$= \lbrace 3,-2,3\rbrace = 3-2Z^{-1}+2Z^{-2}$

Demikian pula, $x_{2}(z) = 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$

Sinyal yang dihasilkan,

$X(Z) = X_{1}(Z)X_{2}(z)$

$= \lbrace 3-2Z^{-1}+2Z^{-2}\rbrace \times \lbrace 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}\rbrace$

$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+6Z^{-4}+6Z^{-5}$

Mengambil transformasi Z terbalik di atas, kita akan mendapatkan sinyal yang dihasilkan sebagai

$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$ Asal di awal

Example 3 - Tentukan konvolusi 2 sinyal berikut -

$x(n) = \lbrace 2,1,0,1\rbrace$

$h(n) = \lbrace 1,2,3,1\rbrace$

Solution -

Mengambil transformasi Z dari sinyal, kita dapatkan,

$x(z) = 2+2Z^{-1}+2Z^{-3}$

Dan $h(n) = 1+2Z^{-1}+3Z^{-2}+Z^{-3}$

Sekarang konvolusi dua sinyal berarti perkalian transformasi Z mereka

Itu adalah $Y(Z) = X(Z) \times h(Z)$

$= \lbrace 2+2Z^{-1}+2Z^{-3}\rbrace \times \lbrace 1+2Z^{-1}+3Z^{-2}+Z^{-3}\rbrace$

$= \lbrace 2+5Z^{-1}+8Z^{-2}+6Z^{-3}+3Z^{-4}+3Z^{-5}+Z^{-6}\rbrace$

Mengambil transformasi Z terbalik, sinyal resultan dapat ditulis sebagai;

$y(n) = \lbrace 2,5,8,6,6,1 \rbrace Originalfirst$

Beberapa sistem memiliki umpan balik dan beberapa tidak. Mereka, yang tidak memiliki sistem umpan balik, keluarannya hanya bergantung pada nilai masukan saat ini. Nilai lampau dari data tidak ada pada saat itu. Jenis sistem ini dikenal sebagai sistem statis. Itu tidak tergantung pada nilai-nilai masa depan juga.

Karena sistem ini tidak memiliki catatan masa lalu, jadi mereka juga tidak memiliki memori. Oleh karena itu, kami mengatakan semua sistem statis adalah sistem tanpa memori. Mari kita ambil contoh untuk memahami konsep ini dengan lebih baik.

Contoh

Mari kita verifikasi apakah sistem berikut adalah sistem statis atau tidak.

$y(t) = x(t)+x(t-1)$
$y(t) = x(2t)$
$y(t) = x = \sin [x(t)]$

Sebuah) $y(t) = x(t)+x(t-1)$

Di sini, x (t) adalah nilai sekarang. Itu tidak ada hubungannya dengan nilai masa lalu. Jadi, ini adalah sistem statis. Namun, dalam kasus x (t-1), jika t = 0, akan berkurang menjadi x (-1) yang merupakan dependen nilai lampau. Jadi, itu tidak statis. Oleh karena itu di sini y (t) bukanlah sistem statis.

b) $y(t) = x(2t)$

Jika kita mengganti t = 2, hasilnya adalah y (t) = x (4). Sekali lagi, ini tergantung pada nilai masa depan. Jadi, ini juga bukan sistem statis.

c) $y(t) = x = \sin [x(t)]$

Dalam ungkapan ini, kita berurusan dengan fungsi sinus. Kisaran fungsi sinus terletak antara -1 hingga +1. Jadi, berapa pun nilai yang kita gantikan untuk x (t), kita akan mendapatkan antara -1 hingga +1. Oleh karena itu, kita dapat mengatakan itu tidak bergantung pada nilai masa lalu atau masa depan. Oleh karena itu, ini adalah sistem statis.

Dari contoh di atas, kita dapat menarik kesimpulan berikut -

Sistem apa pun yang mengalami pergeseran waktu tidak statis.
Semua sistem yang mengalami pergeseran amplitudo juga tidak statis.
Kasus integrasi dan diferensiasi juga tidak statis.

Jika suatu sistem bergantung pada nilai sinyal masa lalu dan masa depan pada saat kapan pun, maka itu dikenal sebagai sistem dinamis. Tidak seperti sistem statis, ini bukan sistem tanpa memori. Mereka menyimpan nilai masa lalu dan masa depan. Oleh karena itu, mereka membutuhkan memori. Mari kita pahami teori ini lebih baik melalui beberapa contoh.

Contoh

Cari tahu apakah sistem berikut ini dinamis.

a) $y(t) = x(t+1)$

Dalam kasus ini, jika t = 1 dimasukkan ke dalam persamaan, maka akan diubah menjadi x (2), yang merupakan nilai dependen masa depan. Karena disini kita memberikan input sebagai 1 tetapi menunjukkan nilai x (2). Karena ini adalah sinyal yang bergantung di masa depan, maka jelas ini adalah sistem dinamis.

b) $y(t) = Real[x(t)]$

$$= \frac{[x(t)+x(t)^*]}{2}$$

Dalam hal ini, berapa pun nilai yang akan kita masukkan itu akan menunjukkan sinyal nilai waktu nyata. Itu tidak memiliki ketergantungan pada nilai masa depan atau masa lalu. Oleh karena itu, ini bukan sistem dinamis melainkan sistem statis.

c) $y(t) = Even[x(t)]$

$$= \frac{[x(t)+x(-t)]}{2}$$

Di sini, jika kita mengganti t = 1, satu sinyal menunjukkan x (1) dan sinyal lainnya akan menampilkan x (-1) yang merupakan nilai lampau. Demikian pula, jika kita menempatkan t = -1 maka satu sinyal akan menampilkan x (-1) dan sinyal lainnya akan menampilkan x (1) yang merupakan nilai masa depan. Oleh karena itu, jelas ini adalah kasus sistem Dinamis.

d) $y(t) = \cos [x(t)]$

Dalam hal ini, karena sistem tersebut adalah fungsi cosinus, ia memiliki domain nilai tertentu yang terletak antara -1 hingga +1. Oleh karena itu, berapa pun nilai yang akan kita masukkan akan kita dapatkan hasilnya dalam batas yang ditentukan. Oleh karena itu, ini adalah sistem statis

Dari contoh di atas, kita dapat menarik kesimpulan berikut -

Semua sinyal kasus pergeseran waktu adalah sinyal dinamis.
Dalam kasus skala waktu juga, semua sinyal adalah sinyal dinamis.
Sinyal kasus integrasi adalah sinyal dinamis.

Sebelumnya, kami melihat bahwa sistem perlu independen dari nilai-nilai masa depan dan masa lalu agar menjadi statis. Dalam hal ini kondisinya hampir sama dengan sedikit modifikasi. Di sini, agar sistem menjadi kausal, ia harus independen dari nilai-nilai masa depan saja. Artinya ketergantungan masa lalu tidak akan menimbulkan masalah bagi sistem untuk menjadi kausal.

Sistem kausal adalah sistem yang dapat direalisasikan secara praktis atau fisik. Mari kita pertimbangkan beberapa contoh untuk memahami ini lebih baik.

Contoh

Mari kita simak sinyal-sinyal berikut ini.

a) $y(t) = x(t)$

Di sini, sinyal hanya bergantung pada nilai x yang sekarang. Misalnya jika kita mengganti t = 3, hasilnya hanya akan ditampilkan untuk saat itu saja. Oleh karena itu, karena tidak bergantung pada nilai masa depan, kita dapat menyebutnya sebagai sistem sebab akibat.

b) $y(t) = x(t-1)$

Di sini, sistem bergantung pada nilai-nilai lampau. Misalnya jika kita mengganti t = 3, ekspresi tersebut akan berkurang menjadi x (2), yang merupakan nilai lampau terhadap masukan kita. Ini tidak tergantung pada nilai-nilai masa depan. Oleh karena itu, sistem ini juga merupakan sistem kausal.

c) $y(t) = x(t)+x(t+1)$

Dalam hal ini, sistem memiliki dua bagian. Bagian x (t), seperti yang telah kita bahas sebelumnya, hanya bergantung pada nilai sekarang. Jadi, tidak ada masalah dengan itu. Namun, jika kita mengambil kasus x (t + 1), itu jelas tergantung pada nilai masa depan karena jika kita menempatkan t = 1, ekspresi tersebut akan berkurang menjadi x (2) yang merupakan nilai masa depan. Oleh karena itu, tidak bersifat kausal.

Sistem non-kausal berlawanan dengan sistem kausal. Jika suatu sistem bergantung pada nilai masukan masa depan setiap saat, maka sistem tersebut dikatakan sistem non-kausal.

Contoh

Mari kita ambil beberapa contoh dan mencoba memahami ini dengan cara yang lebih baik.

a) $y(t) = x(t+1)$

Kami telah membahas sistem ini dalam sistem kausal juga. Untuk input apa pun, itu akan mengurangi sistem ke nilai masa depan. Misalnya, jika t = 2, maka akan berkurang menjadi x (3), yang merupakan nilai masa depan. Oleh karena itu, sistemnya Non-Kausal.

b) $y(t) = x(t)+x(t+2)$

Dalam kasus ini, x (t) murni fungsi dependen nilai sekarang. Kita telah membahas bahwa fungsi x (t + 2) tergantung masa depan karena untuk t = 3 akan memberikan nilai untuk x (5). Oleh karena itu, ini Non-kausal.

c) $y(t) = x(t-1)+x(t)$

Dalam sistem ini, itu tergantung pada nilai sekarang dan masa lalu dari masukan yang diberikan. Apapun nilai yang kita gantikan, tidak akan pernah menunjukkan ketergantungan di masa depan. Jelas, ini bukanlah sistem non-kausal; melainkan sistem kausal.

Sistem anti-kausal hanyalah versi modifikasi dari sistem non-kausal. Sistem hanya bergantung pada nilai input yang akan datang. Itu tidak memiliki ketergantungan baik pada nilai sekarang atau pada masa lalu.

Contoh

Cari tahu apakah sistem berikut ini anti-kausal.

a) $y(t) = x(t)+x(t-1)$

Sistem ini memiliki dua subfungsi. Satu subfungsi x (t + 1) bergantung pada nilai input yang akan datang tetapi subfungsi lain x (t) hanya bergantung pada saat ini. Karena sistem ini bergantung pada nilai sekarang juga di samping nilai masa depan, sistem ini tidak anti-kausal.

b) $y(t) = x(t+3)$

Jika kita menganalisis sistem di atas, kita dapat melihat bahwa sistem hanya bergantung pada nilai masa depan dari sistem yaitu jika kita menempatkan t = 0 maka akan berkurang menjadi x (3), yang merupakan nilai masa depan. Sistem ini adalah contoh sempurna dari sistem anti-kausal.

Sistem linier mengikuti hukum superposisi. Hukum ini diperlukan dan kondisi yang cukup untuk membuktikan linearitas sistem. Selain itu, sistem ini merupakan kombinasi dari dua jenis hukum -

Hukum aditif
Hukum homogenitas

Keduanya, hukum homogenitas dan hukum aditif ditunjukkan pada gambar di atas. Namun, ada beberapa kondisi lain untuk memeriksa apakah sistem tersebut linier atau tidak.

The conditions are -

Output harus nol untuk input nol.
Seharusnya tidak ada operator non-linier yang ada dalam sistem.

Contoh operator non-linier -

(a) Operator trigonometri- Sin, Cos, Tan, Cot, Sec, Cosec dll.

(b) Eksponensial, logaritmik, modulus, persegi, Kubus dll.

Masukan x atau keluaran y tidak boleh memiliki operator non-linier ini.

Contoh

Mari kita cari tahu apakah sistem berikut ini linier.

a) $y(t) = x(t)+3$

Sistem ini bukan sistem linier karena melanggar ketentuan pertama. Jika input kita masukkan nol sehingga x (t) = 0, maka outputnya bukan nol.

b) $y(t) = \sin tx(t)$

Dalam sistem ini, jika kita memberi masukan sebagai nol, keluaran akan menjadi nol. Makanya, kondisi pertama jelas terpenuhi. Sekali lagi, tidak ada operator non-linier yang diterapkan pada x (t). Makanya, syarat kedua juga terpenuhi. Oleh karena itu, sistem tersebut merupakan sistem linier.

c) $y(t) = \sin (x(t))$

Pada sistem di atas kondisi pertama terpenuhi karena jika kita masukkan x (t) = 0 maka outputnya juga akan menjadi sin (0) = 0. Namun kondisi kedua tidak terpenuhi, karena ada operator non linier yang mengoperasikan x (t). Makanya, sistemnya tidak linier.

Jika kita ingin mendefinisikan sistem ini, kita dapat mengatakan bahwa sistem yang tidak linier adalah sistem yang tidak linier. Jelas, semua kondisi, yang dilanggar dalam sistem linier, harus dipenuhi dalam kasus ini.

Kondisi

Output tidak boleh nol ketika input yang diterapkan adalah nol.
Setiap operator non-linier dapat diterapkan pada input atau output untuk membuat sistem menjadi non-linier.

Contoh

Untuk mengetahui apakah sistem yang diberikan linier atau non-linier.

a) $y(t) = e^{x(t)}$

Pada sistem di atas kondisi pertama terpenuhi karena jika kita menjadikan input nol maka outputnya adalah 1. Selain itu, operator eksponensial non linier diterapkan pada input tersebut. Jelas, ini adalah kasus sistem Non-Linear.

b) $y(t) = x(t+1)+x(t-1)$

Jenis sistem di atas berhubungan dengan nilai masa lalu dan masa depan. Namun, jika kita akan menjadikan inputnya nol, maka tidak ada nilainya. Oleh karena itu, kita dapat mengatakan jika inputnya nol, maka waktu yang diskalakan dan versi input waktu bergeser juga akan menjadi nol, yang melanggar ketentuan pertama kita. Sekali lagi, tidak ada operator non-linier. Karena itu, syarat kedua juga dilanggar. Jelaslah, sistem ini bukanlah sistem non-linier; melainkan sistem linier.

Untuk sistem waktu-invariant, keluaran dan masukan harus ditunda oleh beberapa satuan waktu. Setiap penundaan yang diberikan dalam masukan harus tercermin dalam keluaran untuk sistem invarian waktu.

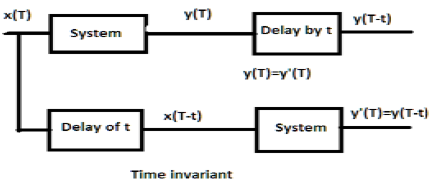
Contoh

a) $y(T) = x(2T)$

Jika ekspresi di atas, pertama kali melewati sistem dan kemudian melalui penundaan waktu (seperti yang ditunjukkan di bagian atas gambar); maka hasilnya akan menjadi$x(2T-2t)$. Sekarang, ekspresi yang sama dilewatkan melalui waktu tunda terlebih dahulu dan kemudian melalui sistem (seperti yang ditunjukkan di bagian bawah gambar). Outputnya akan menjadi$x(2T-t)$.

Oleh karena itu, sistem tersebut bukanlah sistem waktu-invarian.

b) $y(T) = \sin [x(T)]$

Jika sinyal pertama kali melewati sistem dan kemudian melalui proses waktu tunda, keluarannya menjadi $\sin x(T-t)$. Begitu pula jika sistem dilewatkan melalui waktu tunda terlebih dahulu kemudian melalui sistem maka akan dihasilkan keluaran$\sin x(T-t)$. Kita dapat melihat dengan jelas bahwa kedua outputnya sama. Oleh karena itu, sistemnya tidak berubah-ubah waktu.

Untuk sistem varian waktu, juga, keluaran dan masukan harus ditunda oleh beberapa konstanta waktu tetapi penundaan pada masukan tidak boleh mencerminkan pada keluaran. Semua kasus penskalaan waktu adalah contoh sistem varian waktu. Demikian pula, ketika koefisien dalam hubungan sistem adalah fungsi waktu, maka sistem juga merupakan varian waktu.

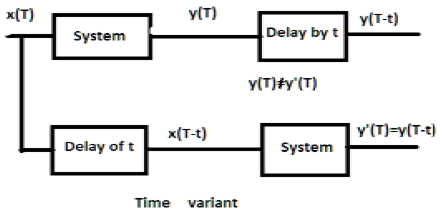
Contoh

a) $y(t) = x[\cos T]$

Jika sinyal di atas pertama kali melewati sistem dan kemudian melalui penundaan waktu, outputnya akan $x\cos (T-t)$. Jika melewati waktu tunda terlebih dahulu dan kemudian melalui sistem, itu akan terjadi$x(\cos T-t)$. Karena keluarannya tidak sama, sistemnya adalah varian waktu.

b) $y(T) = \cos T.x(T)$

Jika ekspresi di atas pertama kali dilewatkan melalui sistem dan kemudian melalui penundaan waktu, maka keluarannya akan $\cos(T-t)x(T-t)$. Namun, jika ekspresi dilewatkan melalui waktu tunda terlebih dahulu dan kemudian melalui sistem, keluarannya akan$\cos T.x(T-t)$. Karena keluarannya tidak sama, jelas sistemnya adalah varian waktu.

Sistem yang stabil memenuhi kondisi BIBO (input terbatas untuk output yang dibatasi). Di sini, batas berarti amplitudo terbatas. Untuk sistem yang stabil, output harus dibatasi atau terbatas, untuk input terbatas atau terbatas, setiap saat.

Beberapa contoh input berbatas adalah fungsi sinus, cosinus, DC, signum dan langkah satuan.

Contoh

a) $y(t) = x(t)+10$

Di sini, untuk input yang dibatasi pasti, kita bisa mendapatkan output yang dibatasi pasti yaitu jika kita meletakkan $x(t) = 2, y(t) = 12$yang terikat di alam. Oleh karena itu, sistemnya stabil.

b) $y(t) = \sin [x(t)]$

Dalam ekspresi yang diberikan, kita tahu bahwa fungsi sinus memiliki batas nilai yang pasti, yang terletak antara -1 hingga +1. Jadi, berapa pun nilai yang akan kita gantikan di x (t), kita akan mendapatkan nilai di dalam batas kita. Oleh karena itu, sistemnya stabil.

Sistem yang tidak stabil tidak memenuhi persyaratan BIBO. Oleh karena itu, untuk input yang dibatasi, kita tidak dapat mengharapkan output yang dibatasi jika sistem tidak stabil.

Contoh

a) $y(t) = tx(t)$

Di sini, untuk masukan yang terbatas, kita tidak dapat mengharapkan keluaran yang terbatas. Misalnya jika kita akan menempatkan$x(t) = 2 \Rightarrow y(t) = 2t$. Ini bukan nilai hingga karena kita tidak mengetahui nilai t. Jadi, bisa direntang dari mana saja. Oleh karena itu, sistem ini tidak stabil. Ini adalah sistem yang tidak stabil.

b) $y(t) = \frac{x(t)}{\sin t}$

Kita telah membahas sebelumnya, bahwa fungsi sinus memiliki rentang tertentu dari -1 hingga +1; tapi di sini, itu ada di penyebut. Jadi pada skenario terburuk, jika t = 0 dan fungsi sinus menjadi nol, maka keseluruhan sistem akan cenderung tak terhingga. Oleh karena itu, jenis sistem ini sama sekali tidak stabil. Jelas, ini adalah sistem yang tidak stabil.

Example 1 - Periksa apakah $y(t) = x*(t)$ linier atau non-linier.

Solution- Fungsi tersebut mewakili konjugasi input. Ini dapat dibuktikan dengan hukum pertama homogenitas dan hukum aditif atau dengan dua aturan. Namun, memverifikasi melalui aturan jauh lebih mudah, jadi kami akan melakukannya.

Jika input ke sistem bernilai nol, maka outputnya juga cenderung nol. Oleh karena itu, syarat pertama kami terpenuhi. Tidak ada operator non-linier yang digunakan baik pada input maupun output. Oleh karena itu, sistemnya adalah Linear.

Example 2 - Periksa apakah $y(t)=\begin{cases}x(t+1), & t > 0\\x(t-1), & t\leq 0\end{cases}$ linier atau non linier

Solution- Jelas, kita dapat melihat bahwa ketika waktu menjadi kurang dari atau sama dengan nol, input menjadi nol. Jadi, kita dapat mengatakan bahwa pada input nol, outputnya juga nol dan kondisi pertama kita terpenuhi.

Sekali lagi, tidak ada operator non-linier yang digunakan pada masukan maupun keluaran. Oleh karena itu, sistemnya adalah Linear.

Example 3 - Periksa apakah $y(t) = \sin t.x(t)$ stabil atau tidak.

Solution - Misalkan, kita mengambil nilai x (t) sebagai 3. Di sini, fungsi sinus telah dikalikan dengannya dan nilai maksimum dan minimum fungsi sinus bervariasi antara -1 hingga +1.

Oleh karena itu, nilai maksimum dan minimum dari seluruh fungsi juga akan bervariasi antara -3 dan +3. Jadi, sistemnya stabil karena di sini kita mendapatkan input yang dibatasi untuk output yang dibatasi.

Discrete Time Fourier Transform (DTFT) ada untuk sinyal energi dan daya. Transformasi-Z juga ada untuk sinyal jenis energi atau Daya (NENP), sampai batas tertentu saja. Penggantian$z=e^{jw}$ digunakan untuk konversi Z-transform ke DTFT hanya untuk sinyal yang benar-benar dapat dijumlahkan.

Jadi, transformasi Z dari sinyal waktu diskrit x (n) dalam deret pangkat dapat ditulis sebagai -

$$X(z) = \sum_{n-\infty}^\infty x(n)Z^{-n}$$

Persamaan di atas mewakili persamaan transformasi Z dua sisi.

Umumnya, ketika sinyal diubah Z, itu dapat direpresentasikan sebagai -

$$X(Z) = Z[x(n)]$$

Atau $x(n) \longleftrightarrow X(Z)$

Jika ini adalah sinyal waktu kontinu, maka transformasi Z tidak diperlukan karena digunakan transformasi Laplace. Namun, sinyal waktu diskrit hanya dapat dianalisis melalui transformasi-Z.

Wilayah Konvergensi

Region of Convergence adalah rentang variabel kompleks Z di bidang Z. Transformasi Z- sinyal terbatas atau konvergen. Jadi, ROC merepresentasikan himpunan nilai Z, di mana X (Z) memiliki nilai terbatas.

Properti ROC

ROC tidak termasuk tiang apa pun.
Untuk sinyal sisi kanan, ROC akan berada di luar lingkaran pada bidang Z.
Untuk sinyal sisi kiri, ROC akan berada di dalam lingkaran pada bidang-Z.
Untuk stabilitas, ROC menyertakan lingkaran unit pada bidang-Z.
Untuk sinyal dua sisi, ROC adalah cincin di bidang-Z.
Untuk sinyal durasi hingga, ROC adalah seluruh bidang-Z.

Transformasi Z secara unik dicirikan oleh -

Ekspresi X (Z)
KOP dari X (Z)

Sinyal dan ROC mereka

x (n)	X (Z)	ROC
$\delta(n)$	$1$	Seluruh pesawat Z.
$U(n)$	$1/(1-Z^{-1})$	Mod (Z)> 1
$a^nu(n)$	$1/(1-aZ^{-1})$	Mod (Z)> Mod (a)
$-a^nu(-n-1)$	$1/(1-aZ^{-1})$	Mod (Z) <Mod (a)
$na^nu(n)$	$aZ^{-1}/(1-aZ^{-1})^2$	Mod (Z)> Mod (a)
$-a^nu(-n-1)$	$aZ^{-1}/(1-aZ^{-1})^2$	Mod (Z) <Mod (a)
$U(n)\cos \omega n$	$(Z^2-Z\cos \omega)/(Z^2-2Z \cos \omega +1)$	Mod (Z)> 1
$U(n)\sin \omega n$	$(Z\sin \omega)/(Z^2-2Z \cos \omega +1)$	Mod (Z)> 1

Contoh

Mari kita temukan Z-transform dan ROC dari sinyal yang diberikan sebagai $x(n) = \lbrace 7,3,4,9,5\rbrace$, di mana asal rangkaiannya adalah 3.

Solution - Menerapkan rumus yang kami miliki -

$X(z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$

$= \sum_{n=-1}^3 x(n)Z^{-n}$

$= x(-1)Z+x(0)+x(1)Z^{-1}+x(2)Z^{-2}+x(3)Z^{-3}$

$= 7Z+3+4Z^{-1}+9Z^{-2}+5Z^{-3}$

ROC adalah seluruh bidang-Z tidak termasuk Z = 0, ∞, -∞

Dalam bab ini, kita akan memahami properti dasar transformasi-Z.

Linearitas

Ini menyatakan bahwa ketika dua atau lebih sinyal diskrit individu dikalikan dengan konstanta, transformasi Z masing-masing juga akan dikalikan dengan konstanta yang sama.

Secara matematis,

$$a_1x_1(n)+a_2x_2(n) = a_1X_1(z)+a_2X_2(z)$$

Proof - Kami tahu itu,

$$X(Z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$$

$= \sum_{n=-\infty}^\infty (a_1x_1(n)+a_2x_2(n))Z^{-n}$

$= a_1\sum_{n = -\infty}^\infty x_1(n)Z^{-n}+a_2\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$

$= a_1X_1(z)+a_2X_2(z)$ (Karenanya Terbukti)

Di sini, ROC adalah $ROC_1\bigcap ROC_2$.

Pergeseran Waktu

Properti pergeseran waktu menggambarkan bagaimana perubahan domain waktu dalam sinyal diskrit akan mempengaruhi domain-Z, yang dapat ditulis sebagai;

$$x(n-n_0)\longleftrightarrow X(Z)Z^{-n}$$

Atau $x(n-1)\longleftrightarrow Z^{-1}X(Z)$

Proof -

Membiarkan $y(P) = X(P-K)$

$Y(z) = \sum_{p = -\infty}^\infty y(p)Z^{-p}$

$= \sum_{p = -\infty}^\infty (x(p-k))Z^{-p}$

Misalkan s = pk

$= \sum_{s = -\infty}^\infty x(s)Z^{-(s+k)}$

$= \sum_{s = -\infty}^\infty x(s)Z^{-s}Z^{-k}$

$= Z^{-k}[\sum_{s=-\infty}^\infty x(m)Z^{-s}]$

$= Z^{-k}X(Z)$ (Karenanya Terbukti)

Di sini, ROC dapat ditulis sebagai Z = 0 (p> 0) atau Z = ∞ (p <0)

Contoh

U (n) dan U (n-1) dapat diplot sebagai berikut

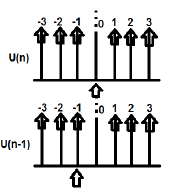
Transformasi-Z U (n) cab ditulis sebagai;

$\sum_{n = -\infty}^\infty [U(n)]Z^{-n} = 1$

Transformasi-Z dari U (n-1) dapat ditulis sebagai;

$\sum_{n = -\infty}^\infty [U(n-1)]Z^{-n} = Z^{-1}$

Jadi disini $x(n-n_0) = Z^{-n_0}X(Z)$ (Karenanya Terbukti)

Penskalaan Waktu

Properti Time Scaling memberi tahu kita, apa yang akan menjadi domain-Z dari sinyal ketika waktu diskalakan dalam bentuk diskritnya, yang dapat ditulis sebagai;

$$a^nx(n) \longleftrightarrow X(a^{-1}Z)$$

Proof -

Membiarkan $y(p) = a^{p}x(p)$

$Y(P) = \sum_{p=-\infty}^\infty y(p)Z^{-p}$

$= \sum_{p=-\infty}^\infty a^px(p)Z^{-p}$

$= \sum_{p=-\infty}^\infty x(p)[a^{-1}Z]^{-p}$

$= X(a^{-1}Z)$(Oleh karena itu terbukti)

ROC: = Mod (ar1) <Mod (Z) <Mod (ar2) dimana Mod = Modulus

Contoh

Mari kita tentukan transformasi-Z dari $x(n) = a^n \cos \omega n$ menggunakan properti Time scaling.

Solution -

Kita sudah tahu bahwa Z-transformasi sinyal $\cos (\omega n)$ diberikan oleh -

$$\sum_{n=-\infty}^\infty(\cos \omega n)Z^{-n} = (Z^2-Z \cos \omega)/(Z^2-2Z\cos \omega +1)$$

Sekarang, menerapkan properti Time scaling, transformasi-Z dari $a^n \cos \omega n$ dapat ditulis sebagai;

$\sum_{n=-\infty}^\infty(a^n\cos \omega n)Z^{-n} = X(a^{-1}Z)$

$= [(a^{-1}Z)^2-(a^{-1}Z \cos \omega n)]/((a^{-1}Z)^2-2(a^{-1}Z \cos \omega n)+1)$

$= Z(Z-a \cos \omega)/(Z^2-2az \cos \omega+a^2)$

Diferensiasi Berturut-turut

Properti Diferensiasi Berturut-turut menunjukkan bahwa transformasi-Z akan terjadi ketika kita membedakan sinyal diskrit dalam domain waktu, sehubungan dengan waktu. Ini ditunjukkan seperti di bawah ini.

$$\frac{dx(n)}{dn} = (1-Z^{-1})X(Z)$$

Proof -

Pertimbangkan LHS dari persamaan - $\frac{dx(n)}{dn}$

$$= \frac{[x(n)-x(n-1)]}{[n-(n-1)]}$$

$= x(n)-X(n-1)$

$= x(Z)-Z^{-1}x(Z)$

$= (1-Z^{-1})x(Z)$ (Karenanya Terbukti)

KOP: R1 <Mod (Z) <R2

Contoh

Mari kita temukan transformasi Z dari sinyal yang diberikan oleh $x(n) = n^2u(n)$

Berdasarkan properti kita bisa menulis

$Zz[nU(n)] = -Z\frac{dZ[U(n)]}{dz}$

$= -Z\frac{d[\frac{Z}{Z-1}]}{dZ}$

$= Z/((Z-1)^2$

$= y(let)$

Sekarang, Z [ny] dapat ditemukan dengan menerapkan kembali properti,

$Z(n,y) = -Z\frac{dy}{dz}$

$= -Z\frac{d[Z/(Z-1)^3]}{dz}$

$= Z(Z+1)/(Z-1)^2$

Lilitan

Ini menggambarkan perubahan dalam domain-Z sistem ketika konvolusi terjadi dalam bentuk sinyal diskrit, yang dapat ditulis sebagai -

$x_1(n)*x_2(n) \longleftrightarrow X_1(Z).X_2(Z)$

Proof -

$X(Z) = \sum_{n = -\infty}^\infty x(n)Z^{-n}$

$= \sum_{n=-\infty}^\infty[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)]Z^{-n}$

$= \sum_{k = -\infty}^\infty x_1(k)[\sum_n^\infty x_2(n-k)Z^{-n}]$

$= \sum_{k = -\infty}^\infty x_1(k)[\sum_{n = -\infty}^\infty x_2(n-k)Z^{-(n-k)}Z^{-k}]$

Misalkan nk = l, maka cab persamaan di atas ditulis sebagai -

$X(Z) = \sum_{k = -\infty}^\infty x_1(k)[Z^{-k}\sum_{l=-\infty}^\infty x_2(l)Z^{-l}]$

$= \sum_{k = -\infty}^\infty x_1(k)X_2(Z)Z^{-k}$

$= X_2(Z)\sum_{k = -\infty}^\infty x_1(Z)Z^{-k}$

$= X_1(Z).X_2(Z)$ (Karenanya Terbukti)

ROC:$ROC\bigcap ROC2$

Contoh

Mari kita temukan konvolusi yang diberikan oleh dua sinyal

$x_1(n) = \lbrace 3,-2,2\rbrace$ ... (persamaan 1)

$x_2(n) = \lbrace 2,0\leq 4\quad and\quad 0\quad elsewhere\rbrace$ ... (persamaan 2)

Transformasi-Z dari persamaan pertama dapat ditulis sebagai;

$\sum_{n = -\infty}^\infty x_1(n)Z^{-n}$

$= 3-2Z^{-1}+2Z^{-2}$

Transformasi-Z dari sinyal kedua dapat ditulis sebagai;

$\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$

$= 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$

Jadi, konvolusi dari dua sinyal di atas diberikan oleh -

$X(Z) = [x_1(Z)^*x_2(Z)]$

$= [3-2Z^{-1}+2Z^{-2}]\times [2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}]$

$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+...\quad...\quad...$

Mengambil transformasi Z terbalik yang kita dapatkan,

$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$

Teorema Nilai Awal

Jika x (n) adalah barisan sebab akibat, yang transformasi Z-nya menjadi X (z), maka teorema nilai awal dapat ditulis sebagai;

$X(n)(at\quad n = 0) = \lim_{z \to \infty} X(z)$

Proof - Kami tahu itu,

$X(Z) = \sum_{n = 0} ^\infty x(n)Z^{-n}$

Memperluas seri di atas, kita dapatkan;

$= X(0)Z^0+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$

$= X(0)\times 1+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$

Dalam kasus di atas jika Z → ∞ maka $Z^{-n}\rightarrow 0$ (Karena n> 0)

Oleh karena itu, kita dapat mengatakan;

$\lim_{z \to \infty}X(z) = X(0)$ (Karenanya Terbukti)

Teorema Nilai Akhir

Teorema Nilai Akhir menyatakan bahwa jika transformasi Z dari suatu sinyal direpresentasikan sebagai X (Z) dan semua kutubnya berada di dalam lingkaran, maka nilai akhirnya dilambangkan sebagai x (n) atau X (∞) dan dapat ditulis sebagai -

$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$

Conditions -

Ini hanya berlaku untuk sistem sebab akibat.
$X(Z)(1-Z^{-1})$ harus memiliki kutub di dalam lingkaran unit di bidang-Z.

Proof - Kami tahu itu

$Z^+[x(n+1)-x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$

$\Rightarrow Z^+[x(n+1)]-Z^+[x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$

$\Rightarrow Z[X(Z)^+-x(0)]-X(Z)^+ = \lim_{k \to \infty}\sum_{n = 0}^kZ^{-n}[x(n+1)-x(n)]$

Di sini, kita dapat menerapkan properti lanjutan Transformasi-Z satu sisi. Jadi, persamaan di atas dapat ditulis ulang menjadi;

$Z^+[x(n+1)] = Z[X(2)^+-x(0)Z^0] = Z[X(Z)^+-x(0)]$

Sekarang dengan menempatkan z = 1 pada persamaan di atas, kita dapat memperluas persamaan di atas -

$\lim_{k \to \infty}{[x(1)-x(0)+x(6)-x(1)+x(3)-x(2)+...\quad...\quad...+x(x+1)-x(k)]}$

Ini dapat dirumuskan sebagai;

$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$(Karenanya Terbukti)

Contoh

Mari kita temukan nilai Awal dan Akhir dari x (n) yang sinyalnya diberikan oleh

$X(Z) = 2+3Z^{-1}+4Z^{-2}$

Solution - Mari kita pertama-tama, cari nilai awal sinyal dengan menerapkan teorema

$x(0) = \lim_{z \to \infty}X(Z)$

$= \lim_{z \to \infty}[2+3Z^{-1}+4Z^{-2}]$

$= 2+(\frac{3}{\infty})+(\frac{4}{\infty}) = 2$

Sekarang mari kita temukan nilai akhir dari sinyal yang menerapkan teorema tersebut

$x(\infty) = \lim_{z \to \infty}[(1-Z^{-1})X(Z)]$

$= \lim_{z \to \infty}[(1-Z^{-1})(2+3Z^{-1}+4Z^{-2})]$

$= \lim_{z \to \infty}[2+Z^{-1}+Z^{-2}-4Z^{-3}]$

$= 2+1+1-4 = 0$

Some other properties of Z-transform are listed below -

Diferensiasi Frekuensi

Ini memberikan perubahan dalam domain-Z dari sinyal, ketika sinyal diskritnya dibedakan terhadap waktu.

$nx(n)\longleftrightarrow -Z\frac{dX(z)}{dz}$

ROC-nya dapat ditulis sebagai;

$r_2< Mod(Z)< r_1$

Contoh

Mari kita temukan nilai x (n) melalui Diferensiasi frekuensi, yang sinyal diskritnya dalam domain Z diberikan oleh $x(n)\longleftrightarrow X(Z) = log(1+aZ^{-1})$

Berdasarkan properti, kita bisa menulisnya

$nx(n)\longleftrightarrow -Z\frac{dx(Z)}{dz}$

$= -Z[\frac{-aZ^{-2}}{1+aZ^{-1}}]$

$= (aZ^{-1})/(1+aZ^{-1})$

$= 1-1/(1+aZ^{-1})$

$nx(n) = \delta(n)-(-a)^nu(n)$

$\Rightarrow x(n) = 1/n[\delta(n)-(-a)^nu(n)]$

Perkalian dalam Waktu

Ini memberikan perubahan dalam domain Z dari sinyal ketika perkalian terjadi pada level sinyal diskrit.

$x_1(n).x_2(n)\longleftrightarrow(\frac{1}{2\Pi j})[X1(Z)*X2(Z)]$

Konjugasi dalam Waktu

Ini menggambarkan representasi sinyal diskrit terkonjugasi dalam domain-Z.

$X^*(n)\longleftrightarrow X^*(Z^*)$

Suatu sistem yang mempunyai fungsi sistem, hanya dapat stabil jika semua kutub berada di dalam lingkaran satuan. Pertama, kami memeriksa apakah sistem itu kausal atau tidak. Jika sistemnya kausal, maka kami melakukan penentuan stabilitas BIBO; dimana stabilitas BIBO mengacu pada input yang dibatasi untuk kondisi output yang dibatasi.

Ini dapat ditulis sebagai;

$Mod(X(Z))< \infty$

$= Mod(\sum x(n)Z^{-n})< \infty$

$= \sum Mod(x(n)Z^{-n})< \infty$

$= \sum Mod[x(n)(re^{jw})^{-n}]< 0$

$= \sum Mod[x(n)r^{-n}]Mod[e^{-jwn}]< \infty$

$= \sum_{n = -\infty}^\infty Mod[x(n)r^{-n}]< \infty$

Persamaan di atas menunjukkan kondisi keberadaan transformasi-Z.

Namun syarat keberadaan sinyal DTFT adalah

$$\sum_{n = -\infty}^\infty Mod(x(n)< \infty$$

Contoh 1

Mari kita coba mencari tahu transformasi Z dari sinyal, yang diberikan sebagai

$x(n) = -(-0.5)^{-n}u(-n)+3^nu(n)$

$= -(-2)^nu(n)+3^nu(n)$

Solution - Di sini, untuk $-(-2)^nu(n)$ ROC adalah Sisi kiri dan Z <2

Untuk $3^nu(n)$ ROC di sisi kanan dan Z> 3

Oleh karena itu, transformasi Z sinyal tidak akan ada karena tidak ada wilayah yang sama.

Contoh 2

Mari kita coba mencari tahu transformasi Z dari sinyal yang diberikan oleh

$x(n) = -2^nu(-n-1)+(0.5)^nu(n)$

Solution - Di sini, untuk $-2^nu(-n-1)$ KOP sinyal adalah Sisi kiri dan Z <2

Untuk sinyal $(0.5)^nu(n)$ ROC adalah sisi kanan dan Z> 0,5

Jadi, ROC umum dibentuk sebagai 0,5 <Z <2

Oleh karena itu, Z-transform dapat ditulis sebagai;

$X(Z) = \lbrace\frac{1}{1-2Z^{-1}}\rbrace+\lbrace\frac{1}{(1-0.5Z)^{-1}}\rbrace$

Contoh 3

Mari kita coba mencari tahu transformasi Z dari sinyal, yang diberikan sebagai $x(n) = 2^{r(n)}$

Solution- r (n) adalah sinyal ramp. Jadi sinyalnya bisa ditulis sebagai;

$x(n) = 2^{nu(n)}\lbrace 1, n<0 (u(n)=0)\quad and\quad2^n, n\geq 0(u(n) = 1)\rbrace$

$= u(-n-1)+2^nu(n)$

Di sini, untuk sinyalnya $u(-n-1)$ dan ROC Z <1 dan untuk $2^nu(n)$ dengan ROC adalah Z> 2.

Jadi, transformasi Z sinyal tidak akan ada.

Z -Transformasi untuk Sistem Kausal

Sistem kausal dapat didefinisikan sebagai $h(n) = 0,n<0$. Untuk sistem kausal, ROC akan berada di luar lingkaran pada bidang Z.

$H(Z) = \displaystyle\sum\limits_{n = 0}^{\infty}h(n)Z^{-n}$

Memperluas persamaan di atas,

$H(Z) = h(0)+h(1)Z^{-1}+h(2)Z^{-2}+...\quad...\quad...$

$= N(Z)/D(Z)$

Untuk sistem kausal, perluasan Fungsi Transfer tidak menyertakan pangkat positif Z. Untuk sistem kausal, urutan pembilang tidak boleh melebihi urutan penyebut. Ini dapat ditulis sebagai-

$\lim_{z \rightarrow \infty}H(Z) = h(0) = 0\quad or\quad Finite$

Untuk kestabilan sistem kausal, kutub-kutub fungsi Transfer harus berada di dalam lingkaran satuan pada bidang-Z.

Z-transform untuk Sistem Anti-kausal

Sistem anti-kausal dapat didefinisikan sebagai $h(n) = 0, n\geq 0$. Untuk sistem Anti kausal, kutub-kutub fungsi transfer harus berada di luar lingkaran satuan pada bidang-Z. Untuk sistem anti kausal, ROC akan berada di dalam lingkaran pada bidang Z.

Jika kita ingin menganalisis sistem, yang sudah direpresentasikan dalam domain frekuensi, sebagai sinyal waktu diskrit maka kita pergi untuk transformasi Z Invers.

Secara matematis, ini dapat direpresentasikan sebagai;

$$x(n) = Z^{-1}X(Z)$$

dimana x (n) adalah sinyal dalam domain waktu dan X (Z) adalah sinyal dalam domain frekuensi.

Jika kita ingin merepresentasikan persamaan di atas dalam format integral maka kita dapat menuliskannya sebagai

$$x(n) = (\frac{1}{2\Pi j})\oint X(Z)Z^{-1}dz$$

Di sini, integral berada di atas lintasan tertutup C. Lintasan ini berada dalam KOP dari x (z) dan memang berisi titik asal.

Metode untuk Menemukan Invers Z-Transform

Ketika analisis diperlukan dalam format diskrit, kami mengubah sinyal domain frekuensi kembali ke format diskrit melalui transformasi Z terbalik. Kami mengikuti empat cara berikut untuk menentukan transformasi Z terbalik.

Metode Divisi Panjang
Metode ekspansi Fraksi Parsial
Metode integral residu atau kontur

Metode Divisi Panjang

Dalam metode ini, transformasi Z dari sinyal x (z) dapat direpresentasikan sebagai rasio polinom seperti yang ditunjukkan di bawah ini;

$$x(z)=N(Z)/D(Z)$$

Sekarang, jika kita terus membagi pembilang dengan penyebut, maka kita akan mendapatkan rangkaian seperti gambar di bawah ini

$$X(z) = x(0)+x(1)Z^{-1}+x(2)Z^{-2}+...\quad...\quad...$$

Urutan di atas mewakili rangkaian transformasi Z terbalik dari sinyal yang diberikan (untuk n≥0) dan sistem di atas adalah kausal.

Namun untuk n <0 deret dapat ditulis sebagai;

$$x(z) = x(-1)Z^1+x(-2)Z^2+x(-3)Z^3+...\quad...\quad...$$

Metode Ekspansi Fraksi Parsial

Di sini juga sinyal diekspresikan pertama kali dalam bentuk N (z) / D (z).

Jika itu adalah pecahan rasional maka akan direpresentasikan sebagai berikut;

$x(z) = b_0+b_1Z^{-1}+b_2Z^{-2}+...\quad...\quad...+b_mZ^{-m})/(a_0+a_1Z^{-1}+a_2Z^{-2}+...\quad...\quad...+a_nZ^{-N})$

Yang di atas tidak tepat jika m <n dan ≠ 0

Jika rasio tersebut tidak tepat (yaitu Tidak tepat), maka kita harus mengubahnya menjadi bentuk yang tepat untuk menyelesaikannya.

Metode Integral Residu atau Kontur

Dalam metode ini, kita mendapatkan invers Z-transform x (n) dengan menjumlahkan residu $[x(z)Z^{n-1}]$di semua kutub. Secara matematis, ini dapat dinyatakan sebagai

$$x(n) = \displaystyle\sum\limits_{all\quad poles\quad X(z)}residues\quad of[x(z)Z^{n-1}]$$

Di sini, residu untuk setiap tiang orde m at $z = \beta$ adalah

$$Residues = \frac{1}{(m-1)!}\lim_{Z \rightarrow \beta}\lbrace \frac{d^{m-1}}{dZ^{m-1}}\lbrace (z-\beta)^mX(z)Z^{n-1}\rbrace$$

Contoh 1

Temukan respon sistem $s(n+2)-3s(n+1)+2s(n) = \delta (n)$, saat semua kondisi awal adalah nol.

Solution - Mengambil transformasi-Z di kedua sisi persamaan di atas, kita dapatkan

$$S(z)Z^2-3S(z)Z^1+2S(z) = 1$$

$\Rightarrow S(z)\lbrace Z^2-3Z+2\rbrace = 1$

$\Rightarrow S(z) = \frac{1}{\lbrace z^2-3z+2\rbrace}=\frac{1}{(z-2)(z-1)} = \frac{\alpha _1}{z-2}+\frac{\alpha _2}{z-1}$

$\Rightarrow S(z) = \frac{1}{z-2}-\frac{1}{z-1}$

Mengambil transformasi Z terbalik dari persamaan di atas, kita dapatkan

$S(n) = Z^{-1}[\frac{1}{Z-2}]-Z^{-1}[\frac{1}{Z-1}]$

$= 2^{n-1}-1^{n-1} = -1+2^{n-1}$

Contoh 2

Tentukan fungsi sistem H (z) dan respons sampel satuan h (n) dari sistem yang persamaan perbedaannya dijelaskan seperti di bawah

$y(n) = \frac{1}{2}y(n-1)+2x(n)$

dimana, y (n) dan x (n) masing-masing adalah keluaran dan masukan dari sistem.

Solution - Mengambil transformasi Z dari persamaan selisih di atas, kita dapatkan

$y(z) = \frac{1}{2}Z^{-1}Y(Z)+2X(z)$

$= Y(Z)[1-\frac{1}{2}Z^{-1}] = 2X(Z)$

$= H(Z) = \frac{Y(Z)}{X(Z)} = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$

Sistem ini memiliki kutub pada $Z = \frac{1}{2}$ dan $Z = 0$ dan $H(Z) = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$

Oleh karena itu, mengambil transformasi Z terbalik di atas, kita dapatkan

$h(n) = 2(\frac{1}{2})^nU(n)$

Contoh 3

Tentukan Y (z), n≥0 dalam kasus berikut -

$y(n)+\frac{1}{2}y(n-1)-\frac{1}{4}y(n-2) = 0\quad given\quad y(-1) = y(-2) = 1$

Solution - Menerapkan Z-transform ke persamaan di atas, kita dapatkan

$Y(Z)+\frac{1}{2}[Z^{-1}Y(Z)+Y(-1)]-\frac{1}{4}[Z^{-2}Y(Z)+Z^{-1}Y(-1)+4(-2)] = 0$

$\Rightarrow Y(Z)+\frac{1}{2Z}Y(Z)+\frac{1}{2}-\frac{1}{4Z^2}Y(Z)-\frac{1}{4Z}-\frac{1}{4} = 0$

$\Rightarrow Y(Z)[1+\frac{1}{2Z}-\frac{1}{4Z^2}] =\frac{1}{4Z}-\frac{1}{2}$

$\Rightarrow Y(Z)[\frac{4Z^2+2Z-1}{4Z^2}] = \frac{1-2Z}{4Z}$

$\Rightarrow Y(Z) = \frac{Z(1-2Z)}{4Z^2+2Z-1}$

Seperti sinyal waktu kontinu Transformasi Fourier, Transformasi Fourier waktu diskrit dapat digunakan untuk merepresentasikan urutan diskrit ke dalam representasi domain frekuensi ekuivalennya dan sistem waktu diskrit LTI serta mengembangkan berbagai algoritme komputasi.

X (jω) dalam FT kontinu, adalah fungsi kontinu dari x (n). Namun, DFT berurusan dengan merepresentasikan x (n) dengan sampel spektrum X (ω). Oleh karena itu, alat matematika ini sangat penting secara komputasi dalam representasi yang nyaman. Baik urutan periodik maupun non-periodik dapat diproses melalui alat ini. Urutan periodik perlu diambil sampelnya dengan memperpanjang periode hingga tak terbatas.

Pengambilan Sampel Domain Frekuensi

Dari pendahuluan, jelas bahwa kita perlu mengetahui bagaimana melanjutkan melalui sampling domain frekuensi yaitu sampling X (ω). Oleh karena itu, hubungan antara transformasi Fourier sampel dan DFT dibentuk dengan cara berikut.

Demikian pula, urutan periodik dapat disesuaikan dengan alat ini dengan memperpanjang periode N hingga tak terbatas.

Biarkan urutan Non periodik menjadi, $X(n) = \lim_{N \to \infty}x_N(n)$

Mendefinisikan transformasi Fouriernya,

$X(\omega ) = \sum_{n=-\infty}^\infty x(n)e^{-jwn}X(K\delta \omega)$

Di sini, X (ω) diambil sampelnya secara berkala, pada setiap interval δω radian.

Karena X (ω) periodik dalam 2π radian, kami hanya memerlukan sampel dalam kisaran fundamental. Sampel diambil setelah interval jarak yang sama dalam rentang frekuensi 0≤ω≤2π. Jarak antara interval yang setara adalah$\delta \omega = \frac{2\pi }{N}k$ radian.

Sekarang mengevaluasi, $\omega = \frac{2\pi}{N}k$

$X(\frac{2\pi}{N}k) = \sum_{n = -\infty}^\infty x(n)e^{-j2\pi nk/N},$ ... persamaan (2)

dimana k = 0,1, …… N-1

Setelah membagi bagian di atas, dan menukar urutan penjumlahan

$X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}[\displaystyle\sum\limits_{l = -\infty}^\infty x(n-Nl)]e^{-j2\pi nk/N}$ ... persamaan (3)

$\sum_{l=-\infty}^\infty x(n-Nl) = x_p(n) = a\quad periodic\quad function\quad of\quad period\quad N\quad and\quad its\quad fourier\quad series\quad = \sum_{k = 0}^{N-1}C_ke^{j2\pi nk/N}$

dimana, n = 0,1,… .., N-1; 'p'- singkatan dari entitas atau fungsi periodik

Koefisien Fourier adalah,

$C_k = \frac{1}{N}\sum_{n = 0}^{N-1}x_p(n)e^{-j2\pi nk/N}$k = 0,1,…, N-1 ... eq (4)

Membandingkan persamaan 3 dan 4, kita dapatkan;

$NC_k = X(\frac{2\pi}{N}k)$k = 0,1,…, N-1 ... eq (5)

$NC_k = X(\frac{2\pi}{N}k) = X(e^{jw}) = \displaystyle\sum\limits_{n = -\infty}^\infty x_p(n)e^{-j2\pi nk/N}$... persamaan (6)

Dari ekspansi seri Fourier,

$x_p(n) = \frac{1}{N}\displaystyle\sum\limits_{k = 0}^{N-1}NC_ke^{j2\pi nk/N} = \frac{1}{N}\sum_{k = 0}^{N-1}X(\frac{2\pi}{N}k)e^{j2\pi nk/N}$... persamaan (7)

Dimana n = 0,1,…, N-1

Di sini, kami mendapat sinyal periodik dari X (ω). $x(n)$ dapat diekstraksi dari $x_p(n)$ hanya, jika tidak ada aliasing di domain waktu. $N\geq L$

N = periode $x_p(n)$ L = periode $x(n)$

$x(n) = \begin{cases}x_p(n), & 0\leq n\leq N-1\\0, & Otherwise\end{cases}$

Pemetaan dilakukan dengan cara ini.

Properti DFT

Linearitas

Ini menyatakan bahwa DFT dari kombinasi sinyal sama dengan jumlah DFT sinyal individu. Mari kita ambil dua sinyal x ₁ (n) dan x ₂ (n), yang DFT-nya adalah X ₁ (ω) dan X ₂ (ω). Jadi jika

$x_1(n)\rightarrow X_1(\omega)$dan$x_2(n)\rightarrow X_2(\omega)$

Kemudian $ax_1(n)+bx_2(n)\rightarrow aX_1(\omega)+bX_2(\omega)$

dimana a dan b adalah konstanta.

Simetri

Properti simetri DFT dapat diturunkan dengan cara yang sama seperti kita menurunkan properti simetri DTFT. Kita tahu bahwa DFT dari barisan x (n) dilambangkan dengan X (K). Sekarang, jika x (n) dan X (K) adalah sekuens bernilai kompleks, maka dapat direpresentasikan sebagai berikut

$x(n) = x_R(n)+jx_1(n),0\leq n\leq N-1$

Dan $X(K) = X_R(K)+jX_1(K),0\leq K\leq N-1$

Properti Dualitas

Mari kita pertimbangkan sinyal x (n), yang DFT-nya diberikan sebagai X (K). Biarkan urutan durasi yang terbatas menjadi X (N). Kemudian menurut teorema dualitas,

Jika, $x(n)\longleftrightarrow X(K)$

Kemudian, $X(N)\longleftrightarrow Nx[((-k))_N]$

Jadi, dengan menggunakan teorema ini jika kita mengetahui DFT, kita dapat dengan mudah menemukan urutan durasi hingga.

Properti Konjugasi Kompleks

Misalkan, ada sinyal x (n), yang DFT-nya juga kita kenal sebagai X (K). Sekarang, jika konjugat kompleks dari sinyal diberikan sebagai x * (n), maka kita dapat dengan mudah mencari DFT tanpa melakukan banyak perhitungan dengan menggunakan teorema di bawah ini.

Jika, $x(n)\longleftrightarrow X(K)$

Kemudian, $x*(n)\longleftrightarrow X*((K))_N = X*(N-K)$

Pergeseran Frekuensi Melingkar

Perkalian deret x (n) dengan deret eksponensial kompleks $e^{j2\Pi kn/N}$setara dengan pergeseran melingkar dari DFT dengan satuan L dalam frekuensi. Ini adalah properti ganda untuk perpindahan waktu melingkar.

Jika, $x(n)\longleftrightarrow X(K)$

Kemudian, $x(n)e^{j2\Pi Kn/N}\longleftrightarrow X((K-L))_N$

Perkalian Dua Urutan

Jika ada dua sinyal x ₁ (n) dan x ₂ (n) dan masing-masing DFT adalah X ₁ (k) dan X ₂ (K), maka perkalian sinyal dalam urutan waktu sesuai dengan konvolusi melingkar dari DFT mereka.

Jika, $x_1(n)\longleftrightarrow X_1(K)\quad\&\quad x_2(n)\longleftrightarrow X_2(K)$

Teorema Parseval

Untuk urutan nilai kompleks x (n) dan y (n), secara umum

Jika, $x(n)\longleftrightarrow X(K)\quad \&\quad y(n)\longleftrightarrow Y(K)$

Kemudian, $\sum_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\sum_{k = 0}^{N-1}X(K)Y^*(K)$

Kami tahu itu kapan $\omega = 2\pi K/N$ dan $N\rightarrow \infty,\omega$ menjadi variabel kontinu dan penjumlahan batas menjadi $-\infty$ untuk $+\infty$.

Karena itu,

$$NC_k = X(\frac{2\pi}{N}k) = X(e^{j\omega}) = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{\frac{-j2\pi nk}{N}} = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{-j\omega n}$$

Transformasi Fourier Waktu Diskrit (DTFT)

Kami tahu itu, $X(e^{j\omega}) = \sum_{n = -\infty}^\infty x(n)e^{-j\omega n}$

Dimana, $X(e^{j\omega})$kontinu dan periodik di ω dan dengan periode 2π. … Persamaan (1)

Sekarang,

$x_p(n) = \sum_{k = 0}^{N-1}NC_ke^{j2 \pi nk/N}$ … Dari seri Fourier

$x_p(n) = \frac{1}{2\pi}\sum_{k=0}^{N-1}NC_ke^{j2\pi nk/N}\times \frac{2\pi}{N}$

ω menjadi kontinu dan $\frac{2\pi}{N}\rightarrow d\omega$, karena alasan yang dikutip di atas.

$x(n) = \frac{1}{2\pi}\int_{n = 0}^{2\pi}X(e^{j\omega})e^{j\omega n}d\omega$… Persamaan (2)

Transformasi Fourier Waktu Diskrit Terbalik

Secara simbolis,

$x(n)\Longleftrightarrow x(e^{j\omega})$(Pasangan Fourier Transform)

Kondisi yang diperlukan dan cukup untuk keberadaan Transformasi Fourier Waktu Diskrit untuk urutan non-periodik x (n) dapat dijumlahkan secara mutlak.

yaitu$\sum_{n = -\infty}^\infty|x(n)|<\infty$

Properti DTFT

Linearity : $a_1x_1(n)+a_2x_2(n)\Leftrightarrow a_1X_1(e^{j\omega})+a_2X_2(e^{j\omega})$
Time shifting - $x(n-k)\Leftrightarrow e^{-j\omega k}.X(e^{j\omega})$
Time Reversal - $x(-n)\Leftrightarrow X(e^{-j\omega})$
Frequency shifting - $e^{j\omega _0n}x(n)\Leftrightarrow X(e^{j(\omega -\omega _0)})$
Differentiation frequency domain - $nx(n) = j\frac{d}{d\omega}X(e^{j\omega})$
Convolution - $x_1(n)*x_2(n)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Multiplication - $x_1(n)\times x_2(n)\Leftrightarrow X_1(e^{j\omega})*X_2(e^{j\omega})$
Co-relation - $y_{x_1\times x_2}(l)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Modulation theorem - $x(n)\cos \omega _0n = \frac{1}{2}[X_1(e^{j(\omega +\omega _0})*X_2(e^{jw})$
Symmetry -$x^*(n)\Leftrightarrow X^*(e^{-j\omega})$ ;

$x^*(-n)\Leftrightarrow X^*(e^{j\omega})$ ;

$Real[x(n)]\Leftrightarrow X_{even}(e^{j\omega})$ ;

$Imag[x(n)]\Leftrightarrow X_{odd}(e^{j\omega})$ ;

$x_{even}(n)\Leftrightarrow Real[x(e^{j\omega})]$ ;

$x_{odd}(n)\Leftrightarrow Imag[x(e^{j\omega})]$ ;
Parseval’s theorem - $\sum_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$

Sebelumnya, kami mempelajari pengambilan sampel dalam domain frekuensi. Dengan pengetahuan dasar itu, kami mengambil sampel$X(e^{j\omega})$dalam domain frekuensi, sehingga analisis digital yang nyaman dapat dilakukan dari data sampel tersebut. Oleh karena itu, DFT diambil sampelnya dalam domain waktu dan frekuensi. Dengan asumsi$x(n) = x_p(n)$

Oleh karena itu, DFT diberikan oleh -

$X(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{-\frac{j2\pi nk}{N}}$, k = 0,1,…., N − 1 … eq (3)

Dan IDFT diberikan oleh -

$X(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k)e^{\frac{j2\pi nk}{N}}$, n = 0,1,…., N − 1 … persamaan (4)

$\therefore x(n)\Leftrightarrow X(k)$

Faktor Twiddle

Ini dilambangkan sebagai $W_N$ dan didefinisikan sebagai $W_N = e^{-j2\pi /N}$. Besarannya selalu dipertahankan pada kesatuan. Fase dari$W_N = -2\pi /N$. Ini adalah vektor pada lingkaran satuan dan digunakan untuk kemudahan komputasi. Secara matematis, ini dapat ditunjukkan sebagai -

$W_N^r = W_N^{r\pm N} = W_N^{r\pm 2N} = ...$

Ini adalah fungsi dari r dan periode N.

Pertimbangkan N = 8, r = 0,1,2,3,… .14,15,16,….

$\Longleftrightarrow W_8^0 = W_8^8 = W_8^{16} = ... = ... = W_8^{32} = ... =1= 1\angle 0$
$W_8^1 = W_8^9 = W_8^{17} = ... = ... = W_8^{33} = ... =\frac{1}{\sqrt 2}= j\frac{1}{\sqrt 2} = 1\angle-\frac{\pi}{4}$

Transformasi Linear

Mari kita pahami Transformasi Linear -

Kami tahu itu,

$DFT(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \sum_{n = 0}^{N-1}x(n).W_n^{-nk};\quad k = 0,1,….,N−1$

$x(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k).W_N^{-nk};\quad n = 0,1,….,N−1$

Note- Perhitungan DFT dapat dilakukan dengan perkalian kompleks N ² dan penambahan kompleks N (N-1).

$x_N = \begin{bmatrix}x(0)\\x(1)\\.\\.\\x(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad x_N$

$X_N = \begin{bmatrix}X(0)\\X(1)\\.\\.\\X(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad X_N$

$\begin{bmatrix}1 & 1 & 1 & ... & ... & 1\\1 & W_N & W_N^2 & ... & ... & W_N^{N-1}\\. & W_N^2 & W_N^4 & ... & ... & W_N^{2(N-1)}\\.\\1 & W_N^{N-1} & W_N^{2(N-1)} & ... & ... & W_N^{(N-1)(N-1)} \end{bmatrix}$

N - titik DFT dalam istilah matriks diberikan oleh - $X_N = W_Nx_N$

$W_N\longmapsto$ Matriks transformasi linier

$Now,\quad x_N = W_N^{-1}X_N$

IDFT dalam bentuk Matriks diberikan oleh

$$x_N = \frac{1}{N}W_N^*X_N$$

Membandingkan kedua ekspresi $x_N,\quad W_N^{-1} = \frac{1}{N}W_N^*$ dan $W_N\times W_N^* = N[I]_{N\times N}$

Karena itu, $W_N$ adalah matriks transformasi linier, matriks ortogonal (kesatuan).

Dari properti periodik $W_N$ dan dari sifat simetrisnya, dapat disimpulkan bahwa, $W_N^{k+N/2} = -W_N^k$

Simetri Melingkar

DFT titik-N dengan durasi terbatas x (n) dengan panjang N≤L, setara dengan DFT titik-N perpanjangan periodik x (n), yaitu $x_p(n)$ periode N. dan $x_p(n) = \sum_{l = -\infty}^\infty x(n-Nl)$. Sekarang, jika kita menggeser urutan, yang merupakan urutan periodik sebanyak k unit ke kanan, diperoleh urutan periodik lain. Ini dikenal sebagai Pergeseran lingkaran dan ini diberikan oleh,

$$x_p^\prime (n) = x_p(n-k) = \sum_{l = -\infty}^\infty x(n-k-Nl)$$

Urutan terbatas baru dapat direpresentasikan sebagai

$$x_p^\prime (n) = \begin{cases}x_p^\prime(n), & 0\leq n\leq N-1\\0 & Otherwise\end{cases}$$

Example - Misalkan x (n) = {1,2,4,3}, N = 4,

$x_p^\prime (n) = x(n-k,modulo\quad N)\equiv x((n-k))_N\quad;ex-if\quad k=2i.e\quad 2\quad unit\quad right\quad shift\quad and\quad N = 4,$

Diasumsikan searah jarum jam sebagai arah positif.

Kita punya, $x\prime(n) = x((n-2))_4$

$x\prime(0) = x((-2))_4 = x(2) = 4$

$x\prime(1) = x((-1))_4 = x(3) = 3$

$x\prime(2) = x((-2))_4 = x(0) = 1$

$x\prime(3) = x((1))_4 = x(1) = 2$

Conclusion - Pergeseran lingkaran urutan titik-N ekuivalen dengan pergeseran linier ekstensi periodiknya dan sebaliknya.

Urutan genap melingkar - $x(N-n) = x(n),\quad 1\leq n\leq N-1$

$i.e.x_p(n) = x_p(-n) = x_p(N-n)$

Konjugasi genap -$x_p(n) = x_p^*(N-n)$

Urutan ganjil melingkar - $x(N-n) = -x(n),\quad 1\leq n\leq N-1$

$i.e.x_p(n) = -x_p(-n) = -x_p(N-n)$

Konjugasi ganjil - $x_p(n) = -x_p^*(N-n)$

Sekarang, $x_p(n) = x_{pe}+x_{po}(n)$, dimana,

$x_{pe}(n) = \frac{1}{2}[x_p(n)+x_p^*(N-n)]$

$x_{po}(n) = \frac{1}{2}[x_p(n)-x_p^*(N-n)]$

Untuk sinyal nyata apa pun x (n),$X(k) = X^*(N-k)$

$X_R(k) = X_R(N-k)$

$X_l(k) = -X_l(N-k)$

$\angle X(k) = -\angle X(N-K)$

Time reversal- membalikkan sampel tentang 0 ^th sampel. Ini diberikan sebagai;

$x((-n))_N = x(N-n),\quad 0\leq n\leq N-1$

Pembalikan waktu adalah memplot contoh urutan, searah jarum jam yaitu diasumsikan arah negatif.

Beberapa Properti Penting Lainnya

Properti IDFT penting lainnya $x(n)\longleftrightarrow X(k)$

Time reversal - $x((-n))_N = x(N-n)\longleftrightarrow X((-k))_N = X(N-k)$
Circular time shift - $x((n-l))_N \longleftrightarrow X(k)e^{j2\pi lk/N}$
Circular frequency shift - $x(n)e^{j2\pi ln/N} \longleftrightarrow X((k-l))_N$
Complex conjugate properties -

$x^*(n)\longleftrightarrow X^*((-k))_N = X^*(N-k)\quad and$

$x^*((-n))_N = x^*(N-n)\longleftrightarrow X^*(-k)$
Multiplication of two sequence -

$x_1(n)\longleftrightarrow X_1(k)\quad and\quad x_2(n)\longleftrightarrow X_2(k)$

$\therefore x_1(n)x_2(n)\longleftrightarrow X_1(k)\quadⓃ X_2(k)$
Circular convolution - dan perkalian dua DFT

$x_1(k)\quad Ⓝ x_2(k) =\sum_{k = 0}^{N-1}x_1(n).x_2((m-n))_n,\quad m = 0,1,2,... .,N-1 $

$x_1(k)\quad Ⓝ x_2(k)\longleftrightarrow X_1(k).X_2(k)$
Circular correlation - Jika $x(n)\longleftrightarrow X(k)$ dan $y(n)\longleftrightarrow Y(k)$ , maka ada urutan korelasi silang yang dilambangkan sebagai $\bar Y_{xy}$ seperti yang $\bar Y_{xy}(l) = \sum_{n = 0}^{N-1}x(n)y^*((n-l))_N = X(k).Y^*(k)$
Parseval’s Theorem - Jika $x(n)\longleftrightarrow X(k)$ dan $y(n)\longleftrightarrow Y(k)$;

$\displaystyle\sum\limits_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\displaystyle\sum\limits_{n =0}^{N-1}X(k).Y^*(k)$

Mari kita ambil dua urutan durasi hingga x ₁ (n) dan x ₂ (n), memiliki panjang bilangan bulat sebagai N. DFT mereka masing-masing adalah X ₁ (K) dan X ₂ (K), yang ditunjukkan di bawah ini -

$$X_1(K) = \sum_{n = 0}^{N-1}x_1(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$ $$X_2(K) = \sum_{n = 0}^{N-1}x_2(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$

Sekarang, kita akan mencoba mencari DFT dari barisan lain x ₃ (n), yang diberikan sebagai X ₃ (K)

$X_3(K) = X_1(K)\times X_2(K)$

Dengan mengambil IDFT di atas kita dapatkan

$x_3(n) = \frac{1}{N}\displaystyle\sum\limits_{n = 0}^{N-1}X_3(K)e^{\frac{j2\Pi kn}{N}}$

Setelah menyelesaikan persamaan di atas, akhirnya kita dapatkan

$x_3(n) = \displaystyle\sum\limits_{m = 0}^{N-1}x_1(m)x_2[((n-m))_N]\quad m = 0,1,2...N-1$

Poin perbandingan	Konvolusi Linear	Konvolusi Melingkar
Bergeser	Pergeseran linier	Pergeseran melingkar
Sampel dalam hasil konvolusi	$N_1+N_2−1$	$Max(N_1,N_2)$
Menemukan respon dari sebuah filter	Bisa jadi	Mungkin tanpa bantalan

Metode Konvolusi Melingkar

Secara umum, ada dua metode, yang diadopsi untuk melakukan konvolusi melingkar dan mereka -

Metode lingkaran konsentris,
Metode perkalian matriks.

Metode Lingkaran Konsentris

Membiarkan $x_1(n)$ dan $x_2(n)$menjadi dua urutan yang diberikan. Langkah-langkah yang diikuti untuk konvolusi melingkar$x_1(n)$ dan $x_2(n)$ adalah

Ambil dua lingkaran konsentris. Plot N sampel$x_1(n)$ pada keliling lingkaran luar (menjaga jarak yang sama titik-titik yang berurutan) berlawanan arah jarum jam.
Untuk merencanakan $x_2(n)$, plot N sampel $x_2(n)$searah jarum jam pada lingkaran dalam, sampel awal ditempatkan pada titik yang sama dengan sampel ^ke- 0$x_1(n)$
Kalikan sampel yang sesuai pada dua lingkaran dan tambahkan untuk mendapatkan keluaran.
Putar lingkaran dalam berlawanan arah jarum jam dengan sampel satu per satu.

Metode Perkalian Matriks

Metode matriks mewakili dua urutan yang diberikan $x_1(n)$ dan $x_2(n)$ dalam bentuk matriks.

Salah satu urutan yang diberikan diulangi melalui pergeseran melingkar dari satu sampel pada satu waktu untuk membentuk matriks NXN.
Urutan lainnya direpresentasikan sebagai matriks kolom.
Perkalian dua matriks menghasilkan konvolusi melingkar.

DFT menyediakan pendekatan alternatif untuk konvolusi domain waktu. Ini dapat digunakan untuk melakukan pemfilteran linier dalam domain frekuensi.

Jadi,$Y(\omega) = X(\omega).H(\omega)\longleftrightarrow y(n)$.

Masalah dalam pendekatan domain frekuensi ini adalah itu $Y(\omega)$, $X(\omega)$ dan $H(\omega)$adalah fungsi berkelanjutan dari ω, yang tidak berguna untuk komputasi digital di komputer. Namun, DFT menyediakan versi sampel dari bentuk gelombang ini untuk menyelesaikan tujuan.

Keuntungannya adalah, memiliki pengetahuan tentang teknik DFT yang lebih cepat seperti FFT, algoritma komputasi yang lebih efisien dapat dikembangkan untuk komputasi komputer digital dibandingkan dengan pendekatan domain waktu.

Pertimbangkan urutan durasi yang terbatas, $[x(n) = 0,\quad for,n<0\quad and\quad n\geq L]$ (persamaan umum), menggairahkan filter linier dengan respons impuls $[h(n) = 0,\quad forn<0\quad and\quad n\geq M]$.

$$x(n)y(n)$$ $$output = y(n) = \sum_{k = 0}^{M-1}h(k).x(n-k)$$

Dari analisis konvolusi, diketahui bahwa durasi y (n) adalah L + M − 1.

Dalam domain frekuensi,

$$Y(\omega) = X(\omega).H(\omega)$$

Sekarang, $Y(\omega)$ adalah fungsi kontinu dari ω dan diambil sampelnya pada satu set frekuensi diskrit dengan jumlah sampel berbeda yang harus sama dengan atau melebihi $L+M-1$.

$$DFT\quad size = N\geq L+M-1$$

Dengan $\omega = \frac{2\pi}{N}k$,

$Y(\omega) = X(k).H(k)$, dimana k = 0,1,…., N-1

Di mana, X (k) dan H (k) masing-masing adalah DFT titik-N dari x (n) dan h (n). $x(n)\& h(n)$ dilapisi dengan angka nol hingga panjang N. Ini tidak akan merusak spektrum kontinu $X(\omega)$ dan $H(\omega)$. Sejak$N\geq L+M-1$, DFT titik-N dari urutan keluaran y (n) cukup untuk merepresentasikan y (n) dalam domain frekuensi dan fakta ini menyimpulkan bahwa perkalian DFT titik-N dari X (k) dan H (k), diikuti dengan perhitungan IDFT N-point harus menghasilkan y (n).

Ini berarti, konvolusi melingkar titik-N dari x (n) dan H (n) dengan bantalan nol, sama dengan konvolusi linier x (n) dan h (n).

Jadi, DFT dapat digunakan untuk penyaringan linier.

Caution - N harus selalu lebih besar dari atau sama dengan $L+M-1$. Jika tidak, efek aliasing akan merusak urutan keluaran.

Misalkan, urutan input x (n) durasi panjang akan diproses dengan sistem yang memiliki respons impuls durasi terbatas dengan menggabungkan kedua urutan. Karena, pemfilteran linier yang dilakukan melalui DFT melibatkan operasi pada blok data ukuran tetap, urutan masukan dibagi menjadi blok data ukuran tetap yang berbeda sebelum diproses.

Blok-blok yang berurutan kemudian diproses satu per satu dan hasilnya digabungkan untuk menghasilkan hasil bersih.

Karena konvolusi dilakukan dengan membagi urutan input panjang menjadi beberapa bagian ukuran tetap yang berbeda, ini disebut konvolusi berpotongan. Urutan masukan yang panjang disegmentasikan ke blok ukuran tetap, sebelum pemrosesan filter FIR.

Dua metode digunakan untuk mengevaluasi konvolusi diskrit -

Overlap-save method
Overlap-add method

Metode Penyimpanan Tumpang Tindih

Overlap-save adalah nama tradisional untuk cara yang efisien untuk mengevaluasi konvolusi diskrit antara sinyal yang sangat panjang x (n) dan filter respon impuls hingga (FIR) h (n). Diberikan di bawah ini adalah langkah-langkah metode penyimpanan Tumpang tindih -

Misalkan panjang blok data masukan = N = L + M-1. Oleh karena itu, DFT dan IDFT panjang = N. Setiap blok data membawa titik data M-1 dari blok sebelumnya diikuti L titik data baru sehingga membentuk urutan data dengan panjang N = L + M-1.

Pertama, DFT titik-N dihitung untuk setiap blok data.
Dengan menambahkan (L-1) nol, respons impuls filter FIR bertambah panjangnya dan titik N DFT dihitung dan disimpan.
Perkalian dua DFT titik-N H (k) dan X _m (k): Y ′ _m (k) = H (k) .X _m (k), dimana K = 0,1,2,… N-1
Kemudian, IDFT [Y ′ _m ((k)] = y ′ ((n) = [y ′ _m (0), y ′ _m (1), y ′ _m (2), ....... y ' _m (M-1), y' _m (M), ....... y ' _m (N-1)]

(di sini, N-1 = L + M-2)
Poin M-1 pertama rusak karena aliasing dan karenanya, mereka dibuang karena catatan data panjangnya N.
Titik L terakhir sama persis dengan hasil konvolusi, jadi

y ′ _m (n) = y _m (n) di mana n = M, M + 1,… .N-1
Untuk menghindari aliasing, yang terakhir M-1 elemen dari setiap record data disimpan dan titik-titik ini membawa ke depan dengan catatan berikutnya dan menjadi 1 ^st M-1 elemen.

Hasil IDFT, di mana M-1 Poin pertama dihindari, untuk membatalkan aliasing dan sisa poin L merupakan hasil yang diinginkan sebagai hasil dari konvolusi linier.

Metode Tambahkan Tumpang-tindih

Diberikan di bawah ini adalah langkah-langkah untuk mengetahui konvolusi diskrit menggunakan metode Tumpang tindih -

Misalkan ukuran blok data masukan menjadi L. Oleh karena itu, ukuran DFT dan IDFT: N = L + M-1

Setiap blok data ditambahkan dengan M-1 nol sampai yang terakhir.
Hitung DFT titik-N.

Dua DFT titik-N dikalikan: Y _m (k) = H (k) .X _m (k), di mana k = 0,, 1,2,…., N-1
IDFT [Y _m (k)] menghasilkan blok dengan panjang N yang tidak terpengaruh oleh aliasing karena ukuran DFT adalah N = L + M-1 dan peningkatan panjang urutan ke titik-N dengan menambahkan nol M-1 ke masing-masing blok.
Poin M-1 terakhir dari setiap blok harus tumpang tindih dan ditambahkan ke poin M-1 pertama dari blok berikutnya.

(alasan: Setiap blok data diakhiri dengan M-1 nol)

Oleh karena itu, metode ini dikenal dengan metode Overlap-add. Jadi, kami mendapatkan -

y (n) = {y ₁ (0), y ₁ (1), y ₁ (2), ... .., y ₁ (L-1), y ₁ (L) + y ₂ (0), y ₁ (L + 1) + y ₂ (1), ... ... .., y ₁ (N-1) + y ₂ (M-1), y ₂ (M), ... .. . ... ... ...}

DCT (Discrete Cosine Transform) adalah urutan masukan-N x (n), 0≤n≤N-1, sebagai transformasi linier atau kombinasi dari eksponensial kompleks. Akibatnya, koefisien DFT secara umum kompleks meskipun x (n) adalah nyata.

Misalkan, kita mencoba mencari transformasi ortogonal yang memiliki struktur N × N yang menyatakan deret nyata x (n) sebagai kombinasi linier deret kosinus. Kami sudah tahu bahwa -

$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$

Dan $x(n) = \frac{1}{N}\sum_{k = 0}^{N-1}x(k)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$

Hal ini dimungkinkan jika urutan titik N x (n) adalah nyata dan genap. Jadi,$x(n) = x(N-n),0\leq n \leq (N-1)$. DFT yang dihasilkan sendiri nyata dan rata. Hal-hal ini memperjelas bahwa kita mungkin dapat merancang transformasi kosinus diskrit, untuk setiap urutan nyata titik N dengan mengambil titik 2N DFT dari urutan "ekstensi genap".

DCT pada dasarnya digunakan dalam pemrosesan gambar dan ucapan. Ini juga digunakan dalam kompresi gambar dan sinyal ucapan.

$DFT[s(n)] = S(k) = \sum_{n = 0}^{2N-1}s(n)W_{2N}^{nk},\quad where\quad 0\leq k \leq 2N-1$

$S(k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)W_{2N}^{nk}+\displaystyle\sum\limits_{n = N}^{2N-1}x(2N-n-1)W_{2N}^{nk};\quad where\quad 0\leq k\leq 2N-1$

$\Rightarrow S(k) = W_{2N}^{-k/2}+\sum_{n = 0}^{N-1}x(n) [W_{2N}^{nk}W_{2N}^{k/2}+W_{2N}^{-nk}W_{2N}^{-k/2}];\quad where\quad 0\leq k\leq 2N-1$

$\Rightarrow S(k) = W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{N}(n+\frac{1}{2})k];\quad where\quad 0\leq k\leq 2N-1$

DCT didefinisikan oleh,

$V(k) = 2\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{2}(n+\frac{1}{2})k]\quad where\quad 0\leq k\leq N-1$

$\Rightarrow V(k) = W_{2N}^{\frac{k}{2}}S(k)\quad or\quad S(k) = W_{2N}^{\frac{k}{2}}V(k),\quad where\quad 0\leq k\leq N-1$

$\Rightarrow V(k) = 2R[W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)W_{2N}^{nk}],\quad where\quad 0\leq k\leq N-1$

Contoh 1

Verifikasi teorema Parseval tentang urutan tersebut $x(n) = \frac{1^n}{4}u(n)$

Solution - $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$

LHS $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2$

$= \displaystyle\sum\limits_{-\infty}^{\infty}x(n)x^*(n)$

$= \displaystyle\sum\limits_{-\infty}^\infty(\frac{1}{4})^{2n}u(n) = \frac{1}{1-\frac{1}{16}} = \frac{16}{15}$

RHS $X(e^{j\omega}) = \frac{1}{1-\frac{1}{4}e-j\omega} = \frac{1}{1-0.25\cos \omega+j0.25\sin \omega}$

$\Longleftrightarrow X^*(e^{j\omega}) = \frac{1}{1-0.25\cos \omega-j0.25\sin \omega}$

Menghitung, $X(e^{j\omega}).X^*(e^{j\omega})$

$= \frac{1}{(1-0.25\cos \omega)^2+(0.25\sin \omega)^2} = \frac{1}{1.0625-0.5\cos \omega}$

$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega$

$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega = 16/15$

Kita dapat melihat bahwa, LHS = RHS. (Karenanya Terbukti)

Contoh 2

Hitung DFT titik-N $x(n) = 3\delta (n)$

Solution - Kami tahu itu,

$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$

$= \displaystyle\sum\limits_{n = 0}^{N-1}3\delta(n)e^{\frac{j2\Pi kn}{N}}$

$ = 3\delta (0)\times e^0 = 1$

Begitu,$x(k) = 3,0\leq k\leq N-1$… Ans.

Contoh 3

Hitung DFT titik-N $x(n) = 7(n-n_0)$

Solution - Kami tahu itu,

$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$

Mensubstitusi nilai x (n),

$\displaystyle\sum\limits_{n = 0}^{N-1}7\delta (n-n_0)e^{-\frac{j2\Pi kn}{N}}$

$= e^{-kj14\Pi kn_0/N}$… Ans

Dalam metode DFT sebelumnya, kita telah melihat bahwa bagian komputasi terlalu panjang. Kami ingin mengurangi itu. Ini dapat dilakukan melalui FFT atau transformasi Fourier cepat. Jadi, kita dapat mengatakan FFT tidak lain adalah komputasi transformasi Fourier diskrit dalam format algoritmik, di mana bagian komputasi akan dikurangi.

Keuntungan utama memiliki FFT adalah melaluinya, kita dapat mendesain filter FIR. Secara matematis, FFT dapat ditulis sebagai berikut;

$$x[K] = \displaystyle\sum\limits_{n = 0}^{N-1}x[n]W_N^{nk}$$

Mari kita ambil contoh untuk memahaminya dengan lebih baik. Kami telah mempertimbangkan delapan poin yang disebutkan dari$x_0\quad to\quad x_7$. Kami akan memilih suku genap dalam satu kelompok dan suku ganjil di kelompok lain. Tampilan diagram di atas dikatakan telah ditunjukkan di bawah ini -

Di sini, poin x ₀ , x ₂ , x ₄ dan x ₆ telah dikelompokkan ke dalam satu kategori dan demikian pula poin x ₁ , x ₃ , x ₅ dan x ₇ dimasukkan ke dalam kategori lain. Sekarang, kita selanjutnya dapat membuatnya dalam kelompok dua dan dapat melanjutkan komputasi. Sekarang, mari kita lihat bagaimana memecah menjadi dua lebih lanjut membantu dalam komputasi.

$x[k] = \displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+\displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_N^{(2r+1)k}$

$= \sum_{r = 0}^{\frac{N}{2}-1}x[2r]W_{N/2}^{rk}+\sum_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_{N/2}^{rk}\times W_N^k$

$= G[k]+H[k]\times W_N^k$

Awalnya, kami mengambil urutan delapan poin, tetapi kemudian kami memecahnya menjadi dua bagian G [k] dan H [k]. G [k] adalah singkatan dari bagian genap sedangkan H [k] adalah singkatan dari bagian ganjil. Jika kita ingin merealisasikannya melalui diagram, maka dapat dilihat seperti dibawah ini -

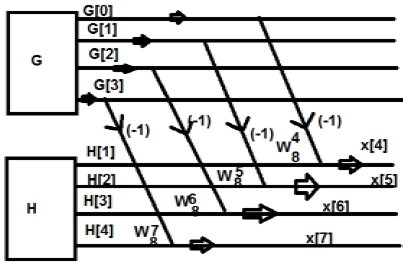
Dari gambar di atas, kita bisa melihat itu

$W_8^4 = -1$

$W_8^5 = -W_8^1$

$W_8^6 = -W_8^2$

$W_8^7 = -W_8^3$

Demikian pula, nilai akhirnya dapat ditulis sebagai berikut -

$G[0]-H[0] = x[4]$

$G[1]-W_8^1H[1] = x[5]$

$G[2]-W_8^2H[2] = x[6]$

$G[1]-W_8^3H[3] = x[7]$

Yang di atas adalah seri periodik. Kerugian dari sistem ini adalah K tidak dapat dipecah melebihi 4 poin. Sekarang Mari kita uraikan di atas menjadi lebih jauh. Kami akan mendapatkan struktur seperti ini

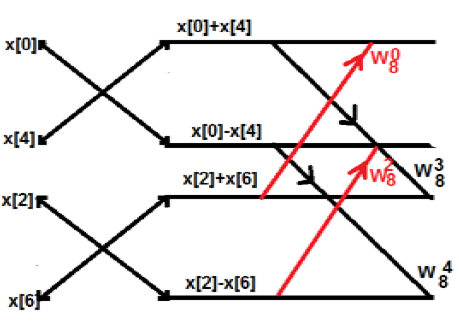
Contoh

Pertimbangkan urutan x [n] = {2,1, -1, -3,0,1,2,1}. Hitung FFT.

Solution - Urutan yang diberikan adalah x [n] = {2,1, -1, -3,0,1,2,1}

Susun istilah seperti yang ditunjukkan di bawah ini;

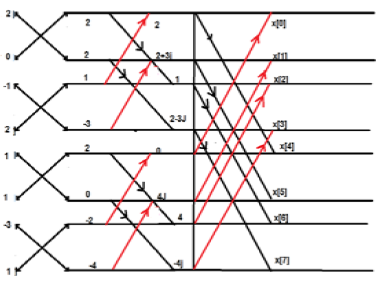
Penggunaan memori yang efisien ini penting untuk merancang perangkat keras yang cepat untuk menghitung FFT. Istilah komputasi di tempat digunakan untuk menggambarkan penggunaan memori ini.

Penipisan dalam Urutan Waktu

Dalam struktur ini, kami merepresentasikan semua titik dalam format biner yaitu dalam 0 dan 1. Kemudian, kami membalikkan struktur tersebut. Urutan yang kita dapatkan setelah itu dikenal sebagai urutan pembalikan bit. Ini juga dikenal sebagai decimation in time sequence. Perhitungan di tempat dari DFT delapan poin ditampilkan dalam format tabel seperti yang ditunjukkan di bawah ini -

POIN	FORMAT BINER	PEMBALIKAN	POIN SETARA
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

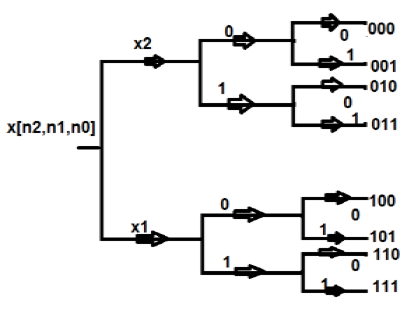
Penipisan dalam Urutan Frekuensi

Selain urutan waktu, urutan titik-N juga dapat direpresentasikan dalam frekuensi. Mari kita ambil urutan empat poin untuk memahaminya dengan lebih baik.

Biarkan urutannya $x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]$. Kami akan mengelompokkan dua poin menjadi satu grup, awalnya. Secara matematis, urutan ini dapat ditulis sebagai;

$$x[k] = \sum_{n = 0}^{N-1}x[n]W_N^{n-k}$$

Sekarang mari kita membuat satu kelompok urutan nomor 0 sampai 3 dan kelompok lain dari urutan 4 sampai 7. Sekarang, secara matematis ini dapat ditunjukkan sebagai;

$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[n]W_N^{nk}+\displaystyle\sum\limits_{n = N/2}^{N-1}x[n]W_N^{nk}$$

Mari kita ganti n dengan r, di mana r = 0, 1, 2…. (N / 2-1). Secara matematis,

$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[r]W_{N/2}^{nr}$$

Kami mengambil empat poin pertama (x [0], x [1], x [2], x [3]) pada awalnya, dan mencoba merepresentasikannya secara matematis sebagai berikut -

$\sum_{n = 0}^3x[n]W_8^{nk}+\sum_{n = 0}^3x[n+4]W_8^{(n+4)k}$

$= \lbrace \sum_{n = 0}^3x[n]+\sum_{n = 0}^3x[n+4]W_8^{(4)k}\rbrace \times W_8^{nk}$

sekarang $X[0] = \sum_{n = 0}^3(X[n]+X[n+4])$

$X[1] = \sum_{n = 0}^3(X[n]+X[n+4])W_8^{nk}$

$= [X[0]-X[4]+(X[1]-X[5])W_8^1+(X[2]-X[6])W_8^2+(X[3]-X[7])W_8^3$

Selanjutnya kita dapat memecahnya menjadi dua bagian lagi, yang berarti alih-alih memecahnya menjadi urutan 4 poin, kita dapat memecahnya menjadi urutan 2 poin.

Filter FIR dapat berguna dalam membuat desain filter dengan bantuan komputer. Mari kita ambil contoh dan lihat cara kerjanya. Diberikan di bawah ini adalah gambar filter yang diinginkan.

Saat melakukan perancangan komputer, kami memecah seluruh gambar grafik kontinu menjadi nilai-nilai diskrit. Dalam batasan tertentu, kami memecahnya menjadi 64, 256 atau 512 (dan seterusnya) jumlah bagian yang memiliki besaran diskrit.

Dalam contoh di atas, kita telah menentukan batas antara -π sampai + π. Kami telah membaginya menjadi 256 bagian. Poin dapat direpresentasikan sebagai H (0), H (1),…. Hingga H (256). Di sini, kami menerapkan algoritma IDFT dan ini akan memberi kami karakteristik fase linier.

Terkadang, kami mungkin tertarik pada beberapa urutan filter tertentu. Katakanlah kita ingin mewujudkan desain yang diberikan di atas melalui filter urutan ^ke- 9 . Jadi, kami mengambil nilai filter sebagai h0, h1, h2… .h9. Secara matematis dapat dilihat seperti di bawah ini

$$H(e^{j\omega}) = h_0+h_1e^{-j\omega}+h_2e^{-2j\omega}+.....+h_9e^{-9j\omega}$$

Di mana ada banyak dislokasi, kami mengambil poin maksimum.

Misalnya, pada gambar di atas, ada penurunan kemiringan yang tiba-tiba antara titik B dan C. Jadi, kami mencoba mengambil lebih banyak nilai diskrit pada titik ini, tetapi ada kemiringan konstan antara titik C dan D. Di sana kami ambil lebih sedikit jumlah nilai diskrit.

Untuk mendesain filter di atas, kami melalui proses minimisasi sebagai berikut;

$H(e^{j\omega1}) = h_0+h_1e^{-j\omega1}+h_2e^{-2j\omega1}+.....+h_9e^{-9j\omega1}$

$H(e^{j\omega2}) = h_0+h_1e^{-j\omega2}+h_2e^{-2j\omega2}+.....+h_9e^{-9j\omega2}$

Demikian pula,

$(e^{j\omega1000}) = h_0+h_1eH^{-j\omega1000}h_2e^{-2j\omega1000}+.....+h_9+e^{-9j\omega1000}$

Mewakili persamaan di atas dalam bentuk matriks, kami memiliki -

$$\begin{bmatrix}H(e^{j\omega_1})\\.\\.\\H(e^{j\omega_{1000}}) \end{bmatrix} = \begin{bmatrix}e^{-j\omega_1} & ... & e^{-j9\omega_1} \\. & & . \\. & & . \\e^{-j\omega_{1000}} &... & e^{j9\omega_{1000}} \end{bmatrix}\begin{bmatrix}h_0\\.\\.\\h_9\end{bmatrix}$$

Mari kita ambil matriks 1000 × 1 sebagai matriks B, matriks 1000 × 9 sebagai A dan matriks 9 × 1 sebagai $\hat{h}$.

Jadi, untuk menyelesaikan matriks di atas, kami akan menulis

$\hat{h} = [A^TA]^{-1}A^{T}B$

$= [A^{*T}A]^{-1}A^{*T}B$

dengan A ^* merepresentasikan konjugat kompleks dari matriks A.

POIN	FORMAT BINER	PEMBALIKAN	POIN SETARA
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

POIN	FORMAT BINER	PEMBALIKAN	POIN SETARA
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

POIN	FORMAT BINER	PEMBALIKAN	POIN SETARA
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7