DSP - Operasi pada Pergeseran Sinyal
Pergeseran berarti pergerakan sinyal, baik dalam domain waktu (sekitar sumbu Y) atau dalam domain amplitudo (di sekitar sumbu X). Oleh karena itu, kita dapat mengklasifikasikan pergeseran menjadi dua kategori yang dinamakan sebagai Pergeseran waktu dan Pergeseran amplitudo, ini selanjutnya dibahas di bawah.
Pergeseran Waktu
Pergeseran waktu berarti pergeseran sinyal dalam domain waktu. Secara matematis, dapat ditulis sebagai
$$ x (t) \ rightarrow y (t + k) $$Nilai K ini bisa positif atau bisa negatif. Menurut tanda nilai k, ada dua jenis perpindahan gigi yang disebut dengan perpindahan kanan dan perpindahan kiri.
Kasus 1 (K> 0)
Ketika K lebih besar dari nol, pergeseran sinyal terjadi ke arah "kiri" dalam domain waktu. Karenanya, jenis perpindahan ini dikenal sebagai Pergeseran Kiri sinyal.
Example
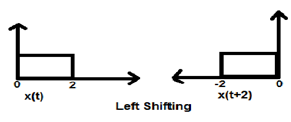
Kasus 2 (K <0)
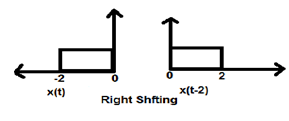
Ketika K kurang dari nol, pergeseran sinyal terjadi ke arah kanan dalam domain waktu. Oleh karena itu, jenis perpindahan ini disebut dengan perpindahan kanan.
Example
Gambar yang diberikan di bawah ini menunjukkan pergeseran kanan sinyal sebesar 2.
Pergeseran Amplitudo
Pergeseran amplitudo berarti pergeseran sinyal dalam domain amplitudo (di sekitar sumbu X). Secara matematis, ini dapat direpresentasikan sebagai -
$$ x (t) \ sisi kanan x (t) + K $$Nilai K ini bisa positif atau negatif. Karenanya, kami memiliki dua jenis pergeseran amplitudo yang selanjutnya dibahas di bawah ini.
Kasus 1 (K> 0)
Ketika K lebih besar dari nol, pergeseran sinyal terjadi ke arah atas pada sumbu x. Oleh karena itu, jenis perpindahan ini disebut dengan perpindahan ke atas.
Example
Mari kita pertimbangkan sinyal x (t) yang diberikan sebagai;
$$ x = \ begin {kasus} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {kasus} $$Mari kita ambil K = + 1 sehingga sinyal baru dapat ditulis sebagai -
$ y (t) \ rightarrow x (t) + 1 $ Jadi, y (t) akhirnya bisa ditulis sebagai;
$$ x (t) = \ begin {cases} 1, & t <0 \\ 2, & 0 \ leq t \ leq 2 \\ 1, & t> 0 \ end {cases} $$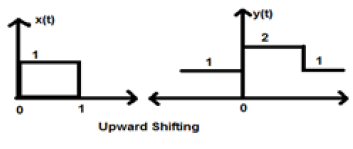
Kasus 2 (K <0)
Ketika K kurang dari nol, pergeseran sinyal terjadi ke arah bawah pada sumbu X. Oleh karena itu, ini disebut pergeseran sinyal ke bawah.
Example
Mari kita pertimbangkan sinyal x (t) yang diberikan sebagai;
$$ x (t) = \ begin {cases} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {cases} $$Mari kita ambil K = -1 sehingga sinyal baru dapat ditulis sebagai;
$ y (t) \ rightarrow x (t) -1 $ Jadi, y (t) akhirnya bisa ditulis sebagai;
$$ y (t) = \ begin {cases} -1, & t <0 \\ 0, & 0 \ leq t \ leq 2 \\ -1, & t> 0 \ end {cases} $$