DSP - Klasifikasi Sinyal CT
Sinyal waktu kontinu dapat diklasifikasikan menurut kondisi atau operasi berbeda yang dilakukan pada sinyal.
Sinyal Genap dan Ganjil
Bahkan Signal
Suatu sinyal dikatakan bahkan jika memenuhi kondisi berikut;
$$ x (-t) = x (t) $$Pembalikan waktu sinyal tidak menyiratkan perubahan apapun pada amplitudo di sini. Misalnya, perhatikan gelombang segitiga yang ditunjukkan di bawah ini.
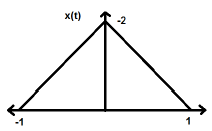
Sinyal segitiga adalah sinyal genap. Karena, sumbu ini simetris terhadap sumbu Y. Kita dapat mengatakan itu adalah bayangan cermin tentang sumbu Y.
Perhatikan sinyal lain seperti yang ditunjukkan pada gambar di bawah ini.
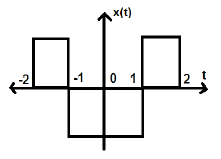
Kita dapat melihat bahwa sinyal di atas sama simetris dengan sumbu Y.
Sinyal Ganjil
Suatu sinyal dikatakan ganjil, jika memenuhi kondisi berikut
$$ x (-t) = -x (t) $$Di sini, baik pembalikan waktu dan perubahan amplitudo terjadi secara bersamaan.
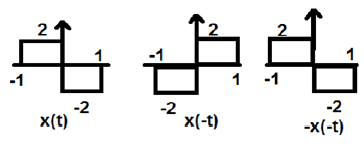
Pada gambar di atas, kita bisa melihat sinyal langkah x (t). Untuk menguji sinyal ganjil atau tidak, pertama kita lakukan pembalikan waktu yaitu x (-t) dan hasilnya seperti yang terlihat pada gambar. Kemudian kita membalik amplitudo dari sinyal yang dihasilkan yaitu –x (-t) dan kita mendapatkan hasil seperti yang ditunjukkan pada gambar.
Jika kita membandingkan bentuk gelombang pertama dan ketiga, kita dapat melihat bahwa keduanya sama, yaitu x (t) = -x (-t), yang memenuhi kriteria kita. Oleh karena itu, sinyal di atas merupakan sinyal Ganjil.
Beberapa hasil penting yang terkait dengan sinyal genap dan ganjil diberikan di bawah ini.
- Genap × Genap = Genap
- Ganjil × Ganjil = Genap
- Genap × Ganjil = Ganjil
- Genap ± Genap = Genap
- Ganjil ± Ganjil = Ganjil
- Genap ± Ganjil = Tidak genap maupun ganjil
Representasi sinyal apa pun ke dalam bentuk genap atau ganjil
Beberapa sinyal tidak dapat langsung diklasifikasikan ke dalam tipe genap atau ganjil. Ini direpresentasikan sebagai kombinasi dari sinyal genap dan ganjil.
$$ x (t) \ kananarrow x_ {e} (t) + x_ {0} (t) $$Dimana x e (t) melambangkan sinyal genap dan x o (t) melambangkan sinyal ganjil
$$ x_ {e} (t) = \ frac {[x (t) + x (-t)]} {2} $$Dan
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$Contoh
Menemukan bagian genap dan ganjil dari sinyal $ x (n) = t + t ^ {2} + t ^ {3} $
Solution - Dari membalikkan x (n), kita dapatkan
$$ x (-n) = -t + t ^ {2} -t ^ {3} $$
Sekarang, menurut rumus, bagian genap
$$ x_ {e} (t) = \ frac {x (t) + x (-t)} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) + (- t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t ^ {2} $$
Demikian pula menurut rumus bagian ganjil adalah
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) - (- t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t + t ^ {3} $$
Sinyal Berkala dan Non Berkala
Sinyal Berkala
Sinyal periodik berulang setelah interval waktu tertentu. Kami dapat menunjukkan ini dalam bentuk persamaan sebagai -
$$ x (t) = x (t) \ pm nT $$Dimana, n = bilangan bulat (1,2,3 ……)
T = Periode waktu fundamental (FTP) ≠ 0 dan ≠ ∞
Periode waktu fundamental (FTP) adalah nilai waktu positif dan tetap terkecil yang sinyalnya bersifat periodik.
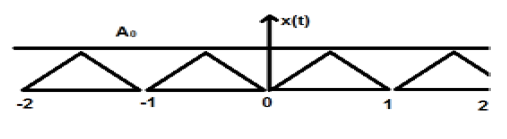
Sinyal segitiga ditunjukkan pada gambar di atas amplitudo A. Di sini, sinyal diulang setiap 1 detik. Oleh karena itu, kita dapat mengatakan bahwa sinyalnya bersifat periodik dan FTP-nya adalah 1 detik.
Sinyal Non-Berkala
Sederhananya, kita dapat mengatakan, sinyal, yang tidak periodik bersifat non-periodik. Jelasnya, sinyal ini tidak akan terulang kembali setelah waktu jeda.
Sinyal non-periodik tidak mengikuti format tertentu; oleh karena itu, tidak ada persamaan matematika tertentu yang dapat mendeskripsikannya.
Sinyal Energi dan Daya
Suatu sinyal dikatakan sebagai sinyal Energi, jika dan hanya jika, energi total yang terkandung terbatas dan bukan nol (0 <E <∞). Oleh karena itu, untuk sinyal jenis energi apa pun, total sinyal yang dinormalisasi adalah terbatas dan bukan nol.
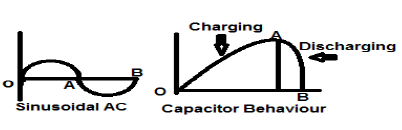
Sinyal arus AC sinusoidal adalah contoh sempurna dari sinyal tipe Energi karena dalam setengah siklus positif dalam satu kasus dan kemudian negatif dalam setengah siklus berikutnya. Oleh karena itu, daya rata-ratanya menjadi nol.
Kapasitor lossless juga merupakan contoh sempurna dari sinyal tipe Energi karena ketika dihubungkan ke sumber, ia mengisi hingga tingkat optimal dan ketika sumber dilepas, ia menghilangkan jumlah energi yang sama melalui beban dan membuat daya rata-ratanya menjadi nol.
Untuk setiap sinyal hingga x (t) energi dapat disimbolkan sebagai E dan ditulis sebagai;
$$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$Densitas spektral sinyal jenis energi memberikan jumlah energi yang didistribusikan pada berbagai tingkat frekuensi.
Sinyal tipe daya
Suatu sinyal dikatakan sebagai sinyal tipe daya, jika dan hanya jika, daya rata-rata yang dinormalisasi adalah terbatas dan bukan nol yaitu (0 <p <∞). Untuk sinyal tipe daya, daya rata-rata yang dinormalisasi terbatas dan bukan nol. Hampir semua sinyal periodik adalah sinyal daya dan daya rata-ratanya terbatas dan bukan nol.
Dalam bentuk matematika, kekuatan sinyal x (t) dapat ditulis sebagai;
$$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$Perbedaan antara Energi dan Sinyal Daya
Tabel berikut merangkum perbedaan Sinyal Energi dan Daya.
| Sinyal daya | Sinyal Energi |
|---|---|
| Sinyal periodik praktis adalah sinyal daya. | Sinyal non-periodik adalah sinyal energi. |
| Di sini, daya rata-rata yang dinormalkan terbatas dan bukan nol. | Di sini, total energi yang dinormalisasi adalah terbatas dan bukan nol. |
| Secara matematis, $$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$ |
Secara matematis, $$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$ |
| Keberadaan sinyal-sinyal ini tidak terbatas dari waktu ke waktu. | Sinyal ini ada untuk jangka waktu terbatas. |
| Energi sinyal daya tidak terbatas selama waktu yang tidak terbatas. | Kekuatan sinyal energi adalah nol selama waktu yang tak terbatas. |
Contoh Terpecahkan
Example 1 - Temukan Kekuatan sinyal $ z (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) + 4 \ sin (3 \ Pi + 30 ^ {o}) $
Solution- Kedua sinyal di atas ortogonal satu sama lain karena istilah frekuensinya identik satu sama lain juga memiliki perbedaan fasa yang sama. Jadi, kekuatan total akan menjadi penjumlahan dari kekuatan individu.
Misalkan $ z (t) = x (t) + y (t) $
Di mana $ x (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) $ dan $ y (t) = 4 \ sin (3 \ Pi + 30 ^ {o}) $
Kekuatan $ x (t) = \ frac {2 ^ {2}} {2} = 2 $
Kekuatan $ y (t) = \ frac {4 ^ {2}} {2} = 8 $
Oleh karena itu, $ P (z) = p (x) + p (y) = 2 + 8 = 10 $ … Ans.
Example 2 - Uji apakah sinyal yang diberikan $ x (t) = t ^ {2} + j \ sin t $ konjugasi atau tidak?
Solution- Di sini, bagian nyata t 2 adalah genap dan bagian ganjil (imajiner) menjadi $ \ sin t $ adalah ganjil. Jadi sinyal di atas adalah sinyal Konjugasi.
Example 3 - Verifikasi apakah $ X (t) = \ sin \ omega t $ adalah sinyal ganjil atau genap.
Solution - Diberikan $ X (t) = \ sin \ omega t $
Dengan pembalikan waktu, kita akan mendapatkan $ \ sin (- \ omega t) $
Tapi kita tahu bahwa $ \ sin (- \ phi) = - \ sin \ phi $.
Karena itu,
$$ \ sin (- \ omega t) = - \ sin \ omega t $$Ini memenuhi kondisi sinyal menjadi ganjil. Oleh karena itu, $ \ sin \ omega t $ adalah sinyal ganjil.