DSP - Operasi pada Diferensiasi Sinyal
Dua operasi yang sangat penting dilakukan pada sinyal adalah Diferensiasi dan Integrasi.
Diferensiasi
Diferensiasi sinyal x (t) berarti representasi kemiringan sinyal tersebut terhadap waktu. Secara matematis, ini direpresentasikan sebagai;
$$ x (t) \ rightarrow \ frac {dx (t)} {dt} $$Dalam kasus diferensiasi OPAMP, metodologi ini sangat membantu. Kami dapat dengan mudah membedakan sinyal secara grafis daripada menggunakan rumus. Namun, syaratnya adalah bahwa sinyal harus berbentuk persegi panjang atau segitiga, yang sering terjadi.
| Sinyal Asli | Sinyal Diferensiasi |
|---|---|
| Lereng | Langkah |
| Langkah | Impuls |
| Impuls | 1 |
Tabel di atas menggambarkan kondisi sinyal setelah dibedakan. Misalnya, sinyal ramp diubah menjadi sinyal langkah setelah diferensiasi. Demikian pula, sinyal langkah satuan menjadi sinyal impuls.
Contoh
Misalkan sinyal yang diberikan kepada kita adalah $ x (t) = 4 [r (t) -r (t-2)] $. Ketika sinyal ini diplot, itu akan terlihat seperti yang ada di sisi kiri gambar yang diberikan di bawah ini. Sekarang, tujuan kami adalah untuk membedakan sinyal yang diberikan.
Untuk memulainya, kita akan mulai mendiferensiasi persamaan yang diberikan. Kita tahu bahwa sinyal ramp setelah diferensiasi memberikan sinyal langkah satuan.
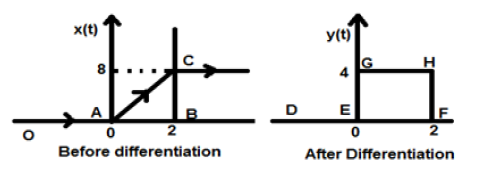
Jadi sinyal yang dihasilkan y (t) dapat ditulis sebagai;
$ y (t) = \ frac {dx (t)} {dt} $
$ = \ frac {d4 [r (t) -r (t-2)]} {dt} $
$ = 4 [u (t) -u (t-2)] $
Sekarang sinyal ini akhirnya diplot, yang ditunjukkan di sisi kanan gambar di atas.