DSP - Transformasi Fourier Cepat
Dalam metode DFT sebelumnya, kita telah melihat bahwa bagian komputasi terlalu panjang. Kami ingin mengurangi itu. Ini dapat dilakukan melalui FFT atau transformasi Fourier cepat. Jadi, kita dapat mengatakan FFT tidak lain adalah komputasi transformasi Fourier diskrit dalam format algoritmik, di mana bagian komputasi akan dikurangi.
Keuntungan utama memiliki FFT adalah melaluinya, kita dapat mendesain filter FIR. Secara matematis, FFT dapat ditulis sebagai berikut;
$$ x [K] = \ displaystyle \ jumlah \ batas_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$Mari kita ambil contoh untuk memahaminya dengan lebih baik. Kami telah mempertimbangkan delapan poin yang dinamai dari $ x_0 \ quad hingga \ quad x_7 $. Kami akan memilih suku genap dalam satu kelompok dan suku ganjil di kelompok lain. Tampilan diagram di atas dikatakan telah ditunjukkan di bawah ini -
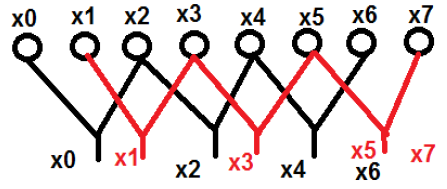
Di sini, poin x 0 , x 2 , x 4 dan x 6 telah dikelompokkan ke dalam satu kategori dan demikian pula poin x 1 , x 3 , x 5 dan x 7 dimasukkan ke dalam kategori lain. Sekarang, kita selanjutnya dapat membuatnya dalam kelompok dua dan dapat melanjutkan komputasi. Sekarang, mari kita lihat bagaimana memecah menjadi dua lebih lanjut membantu dalam komputasi.
$ x [k] = \ displaystyle \ jumlah \ batas_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_N ^ {2rk} + \ displaystyle \ sum \ limit_ {r = 0 } ^ {\ frac {N} {2} -1} x [2r + 1] W_N ^ {(2r + 1) k} $
$ = \ sum_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_ {N / 2} ^ {rk} + \ sum_ {r = 0} ^ {\ frac {N } {2} -1} x [2r + 1] W_ {N / 2} ^ {rk} \ kali W_N ^ k $
$ = G [k] + H [k] \ kali W_N ^ k $
Awalnya, kami mengambil urutan delapan poin, tetapi kemudian kami memecahnya menjadi dua bagian G [k] dan H [k]. G [k] adalah singkatan dari bagian genap sedangkan H [k] adalah singkatan dari bagian ganjil. Jika kita ingin merealisasikannya melalui diagram, maka dapat dilihat seperti dibawah ini -
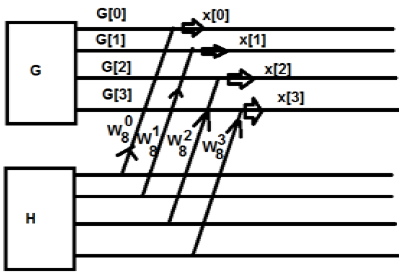
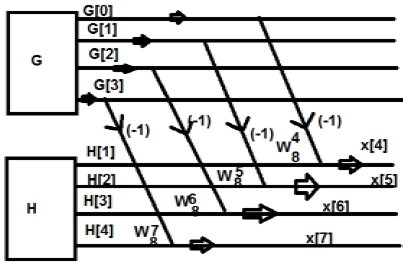
Dari gambar di atas, kita bisa melihat itu
$ W_8 ^ 4 = -1 $
$ W_8 ^ 5 = -W_8 ^ 1 $
$ W_8 ^ 6 = -W_8 ^ 2 $
$ W_8 ^ 7 = -W_8 ^ 3 $
Demikian pula, nilai akhirnya dapat ditulis sebagai berikut -
$ G [0] -J [0] = x [4] $
$ G [1] -W_8 ^ 1H [1] = x [5] $
$ G [2] -W_8 ^ 2H [2] = x [6] $
$ G [1] -W_8 ^ 3H [3] = x [7] $
Yang di atas adalah seri periodik. Kerugian dari sistem ini adalah K tidak dapat dipecah melebihi 4 poin. Sekarang Mari kita uraikan di atas menjadi lebih jauh. Kami akan mendapatkan struktur seperti ini
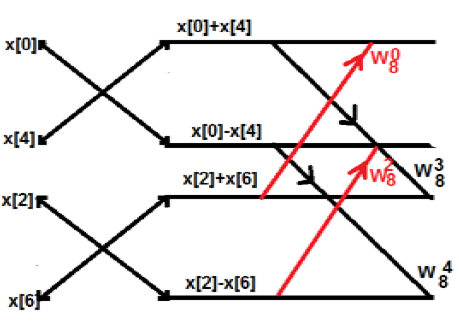
Contoh
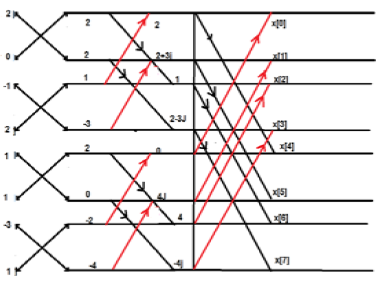
Pertimbangkan urutan x [n] = {2,1, -1, -3,0,1,2,1}. Hitung FFT.
Solution - Urutan yang diberikan adalah x [n] = {2,1, -1, -3,0,1,2,1}
Susun istilah seperti yang ditunjukkan di bawah ini;