DSP - Komputasi Di Tempat
Penggunaan memori yang efisien ini penting untuk merancang perangkat keras yang cepat untuk menghitung FFT. Istilah komputasi di tempat digunakan untuk menggambarkan penggunaan memori ini.
Penipisan dalam Urutan Waktu
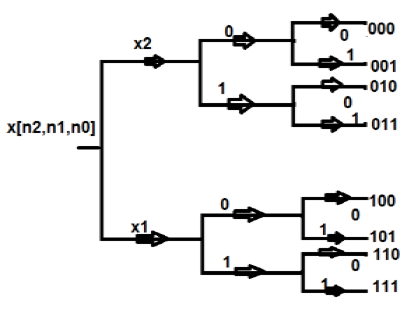
Dalam struktur ini, kami merepresentasikan semua titik dalam format biner yaitu dalam 0 dan 1. Kemudian, kami membalikkan struktur tersebut. Urutan yang kita dapatkan setelah itu dikenal sebagai urutan pembalikan bit. Ini juga dikenal sebagai desimasi dalam urutan waktu. Perhitungan di tempat dari DFT delapan poin ditampilkan dalam format tabel seperti yang ditunjukkan di bawah ini -
| POIN | FORMAT BINER | PEMBALIKAN | POIN SETARA |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
Penipisan dalam Urutan Frekuensi
Selain urutan waktu, urutan titik-N juga dapat direpresentasikan dalam frekuensi. Mari kita ambil urutan empat poin untuk memahaminya dengan lebih baik.
Misalkan urutannya menjadi $ x [0], x [1], x [2], x [3], x [4], x [5], x [6], x [7] $. Kami akan mengelompokkan dua poin menjadi satu grup, awalnya. Secara matematis, urutan ini dapat ditulis sebagai;
$$ x [k] = \ jumlah_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$Sekarang mari kita buat satu kelompok urutan nomor 0 sampai 3 dan kelompok lain dari urutan 4 sampai 7. Sekarang, secara matematis ini dapat ditunjukkan sebagai;
$$ \ displaystyle \ sum \ batas_ {n = 0} ^ {\ frac {N} {2} -1} x [n] W_N ^ {nk} + \ displaystyle \ jumlah \ batas_ {n = N / 2} ^ {T-1} x [n] W_N ^ {nk} $$Mari kita ganti n dengan r, di mana r = 0, 1, 2…. (N / 2-1). Secara matematis,
$$ \ displaystyle \ sum \ batas_ {n = 0} ^ {\ frac {N} {2} -1} x [r] W_ {N / 2} ^ {nr} $$Kami mengambil empat poin pertama (x [0], x [1], x [2], x [3]) pada awalnya, dan mencoba merepresentasikannya secara matematis sebagai berikut -
$ \ sum_ {n = 0} ^ 3x [n] W_8 ^ {nk} + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(n + 4) k} $
$ = \ lbrace \ sum_ {n = 0} ^ 3x [n] + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(4) k} \ rbrace \ times W_8 ^ {nk} $
sekarang $ X [0] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) $
$ X [1] = \ jumlah_ {n = 0} ^ 3 (X [n] + X [n + 4]) W_8 ^ {nk} $
$ = [X [0] -X [4] + (X [1] -X [5]) W_8 ^ 1 + (X [2] -X [6]) W_8 ^ 2 + (X [3] -X [7]) W_8 ^ 3 $
Selanjutnya kita dapat memecahnya menjadi dua bagian lagi, yang berarti alih-alih memecahnya menjadi urutan 4 poin, kita dapat memecahnya menjadi urutan 2 poin.