DSP - Operasi pada Konvolusi Sinyal
Konvolusi dua sinyal dalam domain waktu setara dengan perkalian representasi mereka dalam domain frekuensi. Secara matematis, kita dapat menulis lilitan dua sinyal sebagai
$$ y (t) = x_ {1} (t) * x_ {2} (t) $$ $$ = \ int _ {- \ infty} ^ {\ infty} x_ {1} (p) .x_ {2 } (tp) dp $$Langkah-langkah untuk konvolusi
- Ambil sinyal x 1 (t) dan taruh t = p di situ sehingga menjadi x 1 (p).
- Ambil sinyal x 2 (t) dan lakukan langkah 1 dan jadikan x 2 (p).
- Buatlah pelipatan sinyal yaitu x 2 (-p).
- Lakukan perpindahan waktu dari sinyal di atas x 2 [- (pt)]
- Kemudian lakukan perkalian kedua sinyal tersebut. yaitu $ x_ {1} (p) .x_ {2} [- (p − t)] $
Contoh
Mari kita lakukan konvolusi sinyal langkah u (t) dengan jenisnya sendiri.
$ y (t) = u (t) * u (t) $
$ = \ int _ {- \ infty} ^ {\ infty} [u (p) .u [- (pt)] dp $
Sekarang t ini bisa lebih besar dari atau kurang dari nol, yang ditunjukkan pada gambar di bawah ini
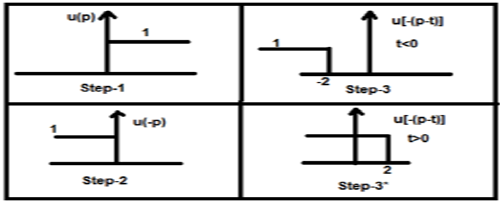
Jadi, dengan kasus di atas, hasilnya muncul dengan kemungkinan sebagai berikut
$ y (t) = \ begin {cases} 0, & if \ quad t <0 \\\ int_ {0} ^ {t} 1dt, & for \ quad t> 0 \ end {cases} $
$ = \ begin {cases} 0, & if \ quad t <0 \\ t, & t> 0 \ end {cases} = r (t) $
Sifat Konvolusi
Komutatif
Ini menyatakan bahwa urutan konvolusi tidak masalah, yang secara matematis dapat ditunjukkan sebagai
$$ x_ {1} (t) * x_ {2} (t) = x_ {2} (t) * x_ {1} (t) $$Asosiatif
Ini menyatakan bahwa urutan konvolusi yang melibatkan tiga sinyal, dapat berupa apa saja. Secara matematis, ini dapat ditampilkan sebagai;
$$ x_ {1} (t) * [x_ {2} (t) * x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t)] * x_ {3} (t) $$Distributif
Dua sinyal dapat ditambahkan terlebih dahulu, dan kemudian konvolusinya dapat dibuat ke sinyal ketiga. Ini setara dengan konvolusi dua sinyal secara individual dengan sinyal ketiga dan akhirnya ditambahkan. Secara matematis, ini dapat ditulis sebagai;
$$ x_ {1} (t) * [x_ {2} (t) + x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t) + x_ {1} ( t) * x_ {3} (t)] $$Daerah
Jika suatu sinyal adalah hasil dari konvolusi dua sinyal maka luas sinyal tersebut adalah perkalian dari sinyal individual tersebut. Secara matematis ini bisa ditulis
Jika $ y (t) = x_ {1} * x_ {2} (t) $
Maka Luas y (t) = Luas x 1 (t) X Luas x 2 (t)
Penskalaan
Jika dua sinyal diskalakan ke beberapa konstanta "a" yang tidak diketahui dan konvolusi dilakukan, sinyal resultan juga akan dikonvolusi ke konstanta "a" yang sama dan akan dibagi dengan kuantitas tersebut seperti yang ditunjukkan di bawah ini.
Jika, $ x_ {1} (t) * x_ {2} (t) = y (t) $
Kemudian, $ x_ {1} (at) * x_ {2} (at) = \ frac {y (at)} {a}, a \ ne 0 $
Menunda
Misalkan sinyal y (t) adalah hasil dari konvolusi dua sinyal x1 (t) dan x2 (t). Jika kedua sinyal masing-masing tertunda oleh waktu t1 dan t2, maka sinyal resultan y (t) akan ditunda oleh (t1 + t2). Secara matematis, dapat ditulis sebagai -
Jika, $ x_ {1} (t) * x_ {2} (t) = y (t) $
Kemudian, $ x_ {1} (t-t_ {1}) * x_ {2} (t-t_ {2}) = y [t- (t_ {1} + t_ {2})] $
Contoh Terpecahkan
Example 1 - Tentukan konvolusi sinyal u (t-1) dan u (t-2).
Solution- Sinyal yang diberikan adalah u (t-1) dan u (t-2). Konvolusi mereka dapat dilakukan seperti yang ditunjukkan di bawah ini -
$ y (t) = u (t-1) * u (t-2) $
$ y (t) = \ int _ {- \ infty} ^ {+ \ infty} [u (t-1) .u (t-2)] dt $
$ = r (t-1) + r (t-2) $
$ = r (t-3) $
Example 2 - Temukan konvolusi dua sinyal yang diberikan oleh
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$ x_ {2} (n) = \ begin {cases} 2, & 0 \ leq n \ leq 4 \\ 0, & x> di tempat lain \ end {case} $
Solution -
x 2 (n) dapat diterjemahkan sebagai $ x_ {2} (n) = \ lbrace 2,2,2,2,2 \ rbrace Originalfirst $
x 1 (n) sebelumnya diberikan $ = \ lbrace 3, -2,3 \ rbrace = 3-2Z ^ {- 1} + 2Z ^ {- 2} $
Demikian pula, $ x_ {2} (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4} $
Sinyal yang dihasilkan,
$ X (Z) = X_ {1} (Z) X_ {2} (z) $
$ = \ lbrace 3-2Z ^ {- 1} + 2Z ^ {- 2} \ rbrace \ times \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {-4} \ brace $
$ = 6 + 2Z ^ {- 1} + 6Z ^ {- 2} + 6Z ^ {- 3} + 6Z ^ {- 4} + 6Z ^ {- 5} $
Mengambil transformasi Z terbalik di atas, kita akan mendapatkan sinyal yang dihasilkan sebagai
$ x (n) = \ lbrace 6,2,6,6,6,0,4 \ rbrace $ Origin di awal
Example 3 - Tentukan konvolusi 2 sinyal berikut -
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution -
Mengambil transformasi Z dari sinyal, kita dapatkan,
$ x (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 3} $
Dan $ h (n) = 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} $
Sekarang konvolusi dua sinyal berarti perkalian transformasi Z mereka
Yaitu $ Y (Z) = X (Z) \ kali h (Z) $
$ = \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 3} \ rbrace \ times \ lbrace 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} \ rbrace $
$ = \ lbrace 2 + 5Z ^ {- 1} + 8Z ^ {- 2} + 6Z ^ {- 3} + 3Z ^ {- 4} + 3Z ^ {- 5} + Z ^ {- 6} \ rbrace $
Mengambil transformasi Z terbalik, sinyal resultan dapat ditulis sebagai;
$ y (n) = \ lbrace 2,5,8,6,6,1 \ rbrace Originalfirst $