Pemrosesan Sinyal Digital - Sinyal DT Dasar

Kita telah melihat bagaimana sinyal dasar dapat direpresentasikan dalam domain waktu kontinu. Mari kita lihat bagaimana sinyal dasar dapat direpresentasikan dalam Domain Waktu Diskrit.

Urutan Impuls Unit

Ini dilambangkan sebagai δ (n) dalam domain waktu diskrit dan dapat didefinisikan sebagai;

$$ \ delta (n) = \ begin {cases} 1, & for \ quad n = 0 \\ 0, & Sebaliknya \ end {cases} $$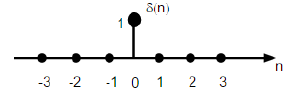

Sinyal Langkah Satuan

Sinyal langkah satuan waktu diskrit didefinisikan sebagai;

$$ U (n) = \ begin {cases} 1, & untuk \ quad n \ geq0 \\ 0, & untuk \ quad n <0 \ end {cases} $$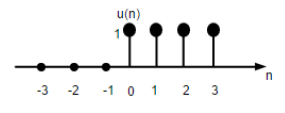

Gambar di atas menunjukkan representasi grafis dari fungsi langkah diskrit.

Fungsi Ramp Unit

Fungsi ramp unit diskrit dapat didefinisikan sebagai -

$$ r (n) = \ mulai {kasus} n, & untuk \ quad n \ geq0 \\ 0, & untuk \ quad n <0 \ end {kasus} $$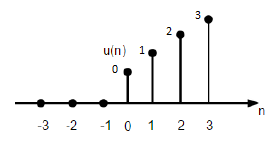

Gambar yang diberikan di atas menunjukkan representasi grafis dari sinyal ramp diskrit.

Fungsi Parabola

Fungsi parabola unit diskrit dilambangkan sebagai p (n) dan dapat didefinisikan sebagai;

$$ p (n) = \ begin {cases} \ frac {n ^ {2}} {2}, & untuk \ quad n \ geq0 \\ 0, & untuk \ quad n <0 \ end {cases} $$

Dalam istilah fungsi unit step dapat ditulis sebagai;

$$ P (n) = \ frac {n ^ {2}} {2} U (n) $$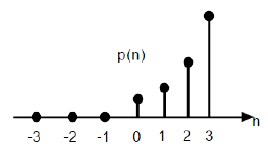

Gambar yang diberikan di atas menunjukkan representasi grafis dari urutan parabola.

Sinyal Sinusoidal

Semua sinyal waktu kontinu bersifat periodik. Urutan sinusoidal waktu-diskrit mungkin atau mungkin tidak periodik. Mereka bergantung pada nilai ω. Agar sinyal waktu diskrit menjadi periodik, frekuensi sudut ω harus merupakan kelipatan rasional 2π.