के बेहतर अभिसरण के लिए स्टर्न-ब्रोकोट पेड़ को नियोजित किया जा सकता है $2^m/3^n$?
पहले से पढ़ने:
- क्या किसी सकारात्मक वास्तविक का अनुमान लगाया जा सकता है? $2^m/3^n$ साथ से $(m,n)$ बहुत पर्याप्त?
- स्टर्न ब्रोकोट पेड़ अनुक्रम
कारण है कि मैं एक ऐसी प्रक्रिया की तलाश कर रहा हूं जिसमें यह खामी न हो, यानी जहां अगला सन्निकटन हमेशा वांछित परिणाम के करीब हो। यही मैंने अब तक कोशिश की है।
प्रश्न (2.) के अनुसार, प्रत्येक सकारात्मक वास्तविक संख्या के लिए$0 \lt g \lt 1$, स्टर्न ब्रोकोट पेड़ [..] में एक अनंत अनुक्रम मौजूद है जो वास्तविक संख्या में परिवर्तित हो जाता है। इस बीच, इस सवाल का एक उत्तर है , और इसमें मुख्य परिणाम निम्नानुसार है: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ प्रश्न (1.) के मद्देनजर, हम विकल्प देते हैं $\ln(2)/\ln(3)$ उस नंबर के लिए $g$। तो यह इस प्रकार है: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$स्टर्न-ब्रोकोट पेड़ के माध्यम से खोज की जा सकती है। ब्लू लाइन फंक्शन है $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, छोटे घेरे भिन्न होते हैं, एक ग्रिड पर मैप किए जाते हैं $\,m/n \to (m,n)\,$, बड़े पैमाने पर काले भरे डॉट्स स्टर्न-ब्रोकोट पेड़ में अंश हैं। यह देखा गया है कि पेड़ के माध्यम से खोज करने से अधिक कुशल है $m$ तथा $n$ एक समय में एक वेतन वृद्धि के साथ।
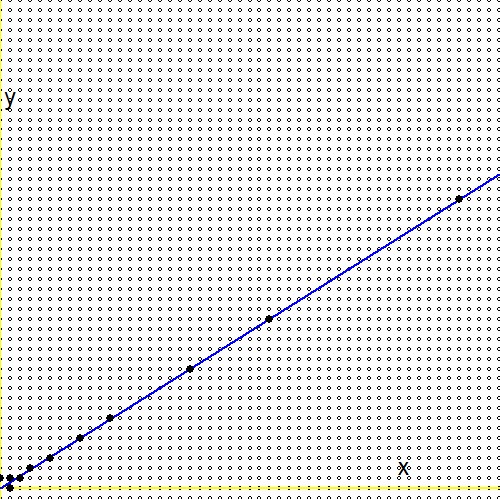
अब उपर्युक्त सूत्रों की दूसरी पंक्ति में अभिव्यक्ति की तुलना संदर्भ में एक समान अभिव्यक्ति के साथ करें (1.): $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ और एक निराशा के लिए तैयार रहें: मनमाना वास्तविक का लघुगणक $r$लापता है! या वैकल्पिक रूप से:$\ln(r)=0$ या $r=1$। इसका मतलब यह है कि स्टर्न-ब्रोकोट पेड़ के माध्यम से हमारी "अनंत खोज", हालांकि अत्यधिक कुशल है, अंत में केवल नंबर एक के लिए एक अनुमान पर आता है। मुझे यह अजीब लगता है, क्योंकि - रेखांकन - वहाँ के बीच एक महान अंतर नहीं लगता है$\color{red}{2^m/3^n \to r}$ तथा $\color{blue}{2^m/3^n \to 1}$:
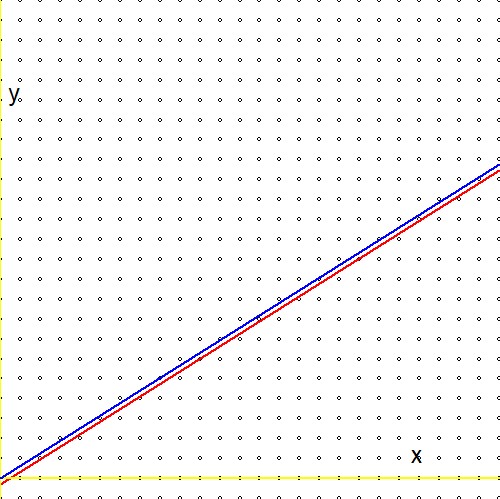
इसलिए प्रश्न: क्या स्टर्न-ब्रोकोट प्रक्रिया को अपनाने के लिए कोई साधन मौजूद है जैसे कि यह एक के अलावा अन्य के लिए काम करता है?
संपादित करें।
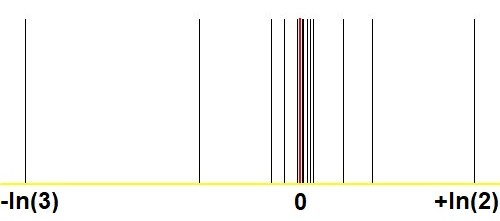
यहाँ एक और ग्राफ आता है जो मेरे Q & A में अनुरूप चित्रों की तुलना में स्टर्न-ब्रोच विधि के साथ आश्चर्यजनक रूप से अभिसरण दर्शाता है, क्या कोई सकारात्मक वास्तविक रूप में अनुमानित किया जा सकता है$2^m/3^n$ साथ से $(m,n)$बहुत पर्याप्त? :
जवाब
मैं एक दृष्टिकोण दूँगा जो स्टर्न-ब्रोच प्रक्रिया का उपयोग नहीं करता है।
यह दिखाने के लिए पर्याप्त है $\frac{2^{m}}{3^{n}}$अंतराल में घना है [1,2]। चूंकि ले रहे हैं$\alpha\in (0,\infty)$ इस अंतराल के बाहर कुछ है $k\in Z$ ताकि $\alpha = 2^{k}\gamma $ कुछ के लिए $\gamma \in [1,2]$। तब हम जानते हैं कि इसमें एक क्रम है$\frac{2^{m}}{3^{n}}$ कौन सा दृष्टिकोण $\gamma$, क्रम को सही से गुणा करें $2^{k}$ (संभवतः अनुक्रम की एक पूंछ लेते हुए), हमें एक अनुक्रम मिलता है $\frac{2^{m}}{3^{n}}$ कौन सा दृष्टिकोण $\alpha$।
अगला विचार है कि नक्शा $f:[1,2] -> [0,1]$ साथ से $f(x) = log_{2}(x)$ एक आपत्ति है।
की छवि $\frac{2^{m}}{3^{n}}$ नक्शे के तहत है $N-Nlog_{2}(3)$। तो यह दिखाने के लिए पर्याप्त है$N-Nlog_{2}(3)$ में घना है $[0,1]$।
यह वीइल के इक्विडिस्ट्रिब्यूशन प्रमेय का परिणाम है, जो एर्गोडिक प्रमेय का एक विशेष मामला है।
विचार करें $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, तोह फिर $a$ सेट की छवि में है, तो है $na = log_{2}(\frac{4^{n}}{3^{n}})$ और इसलिए इसका आंशिक हिस्सा है $na$।
वीइल इक्विडिस्टेनेशन प्रमेय (जो एक तुच्छ परिणाम नहीं है) दर्शाता है कि अपरिमेय के भिन्नात्मक भाग के लिए $na$समान रूप से वितरित किया जाता है और इसलिए [0,1] पर घना होता है। जबसे$2-log_{2}(3)$ तर्कहीन है आप इस प्रमेय का उपयोग कर सकते हैं।