統計-箱ひげ図

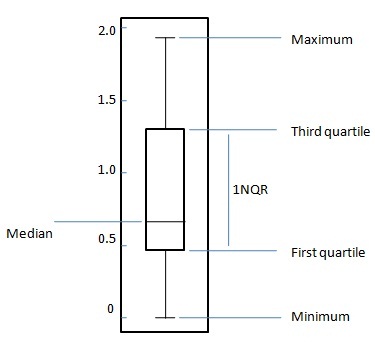
箱ひげ図は、次の5つの数値の要約に基づいてデータの分布を表示するための標準化された方法です。

1. Minimum

2. 最初の四分位数

3. Median

4. 第3四分位

5. Maximum

箱ひげ図の一様分布データセットの場合、中央の長方形は、最初の四分位数から3番目の四分位数（または四分位範囲、IQR）にまたがっています。長方形の内側の線は中央値を示し、ボックスの上下の「ひげ」は最小値と最大値の位置を示します。このような箱ひげ図は、最小から最大までの変動の全範囲、変動の可能性のある範囲、IQR、および中央値を表示します。

問題文：

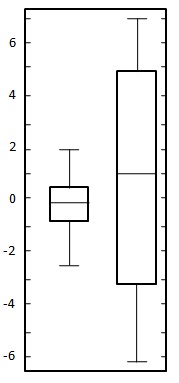
次の2つのデータセットの箱ひげ図を作成します。

0.22
-0.87
-2.39
-1.79
0.37
-1.54
1.28
-0.31
-0.74
1.72
0.38
-0.17
-0.62
-1.10
0.30
0.15
2.30
0.19
-0.50
-0.09

-5.13
-2.19
-2.43
-3.83
0.50
-3.25
4.32
1.63
5.18
-0.43
7.11
4.87
-3.10
-5.81
3.76
6.31
2.58
0.07
5.76
3.50

解決：

ここでは、両方のデータセットがゼロ付近で均一にバランスが取れているため、平均はほぼゼロです。最初のデータセットの変動範囲は約-2.5〜2.5ですが、2番目のデータセットの範囲は約-6〜6です。以下に示すようにグラフを描画します。