統計-ガンマ分布
ガンマ分布は、2パラメーターファミリーの連続確率分布を表します。ガンマ分布は、一般的に3種類のパラメーターの組み合わせで考案されます。
形状パラメータ$ k $とスケールパラメータ$ \ theta $。
形状パラメーター$ \ alpha = k $および逆スケールパラメーター$ \ beta = \ frac {1} {\ theta} $は、レートパラメーターと呼ばれます。
形状パラメータ$ k $と平均パラメータ$ \ mu = \ frac {k} {\ beta} $。
各パラメーターは正の実数です。ガンマ分布は、次の基準によって駆動される最大エントロピー確率分布です。
式
$ {E [X] = k \ theta = \ frac {\ alpha} {\ beta} \ gt 0 \および\は\固定されています。\\ [7pt] E [ln(X)] = \ psi(k)+ ln(\ theta)= \ psi(\ alpha)-ln(\ beta)\および\は\固定されています。} $
ここで-
$ {X} $ =確率変数。
$ {\ psi} $ =ディガンマ関数。
形状$ \ alpha $とレート$ \ beta $を使用した特性評価
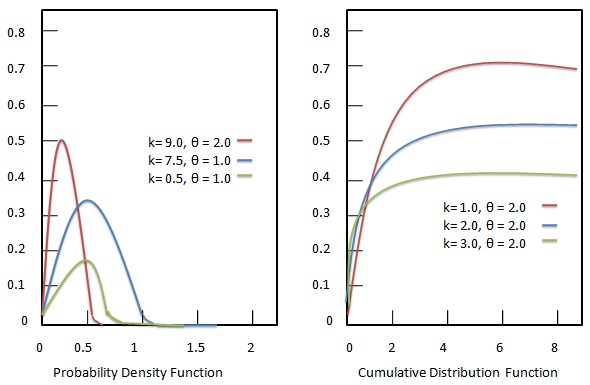
確率密度関数
ガンマ分布の確率密度関数は次のように与えられます。
式
ここで-
$ {\ alpha} $ =位置パラメータ。
$ {\ beta} $ =スケールパラメータ。
$ {x} $ =確率変数。
累積分布関数
ガンマ分布の累積分布関数は次のように与えられます。
式
$ {F(x; \ alpha、\ beta)= \ int_0 ^ xf(u; \ alpha、\ beta)du = \ frac {\ gamma(\ alpha、\ beta x)} {\ Gamma(\ alpha)} } $
ここで-
$ {\ alpha} $ =位置パラメータ。
$ {\ beta} $ =スケールパラメータ。
$ {x} $ =確率変数。
$ {\ gamma(\ alpha、\ beta x)} $ =不完全ガンマ関数を下げます。
形状$ k $とスケール$ \ theta $を使用した特性評価
確率密度関数
ガンマ分布の確率密度関数は次のように与えられます。
式
ここで-
$ {k} $ =形状パラメータ。
$ {\ theta} $ =スケールパラメータ。
$ {x} $ =確率変数。
$ {\ Gamma(k)} $ = kで評価されたガンマ関数。
累積分布関数
ガンマ分布の累積分布関数は次のように与えられます。
式
$ {F(x; k、\ theta)= \ int_0 ^ xf(u; k、\ theta)du = \ frac {\ gamma(k、\ frac {x} {\ theta})} {\ Gamma(k )}} $
ここで-
$ {k} $ =形状パラメータ。
$ {\ theta} $ =スケールパラメータ。
$ {x} $ =確率変数。
$ {\ gamma(k、\ frac {x} {\ theta})} $ =不完全ガンマ関数を下げます。