統計-残余分析

残差分析は、残差を定義し、残差プロットグラフを調べることにより、線形回帰モデルの適切性を評価するために使用されます。

残余

残余（$ e $）は、観測値（$ y $）と予測値（$ \ hat y $）の差を指します。すべてのデータポイントには1つの残差があります。

偏残差プロット

残差プロットは、残差が縦軸にあり、独立変数が横軸にあるグラフです。ドットが横軸の周りにランダムに分散している場合は、線形回帰モデルがデータに適しています。それ以外の場合は、非線形モデルを選択します。

偏残差プロットの種類

次の例は、残余プロットのいくつかのパターンを示しています。

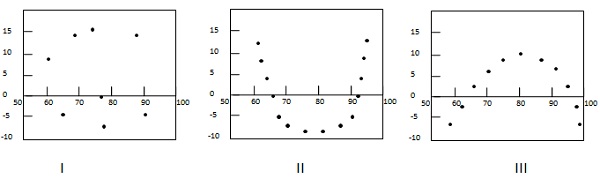
最初のケースでは、ドットはランダムに分散しています。したがって、線形回帰モデルが推奨されます。2番目と3番目のケースでは、ドットはランダムに分散しておらず、非線形回帰法が好ましいことを示唆しています。

例

Problem Statement:

次のデータに対して線形回帰モデルが適切な場所を確認します。

$ x $	60	70	80	85	95
$ y $（実際の値）	70	65	70	95	85
$ \ hat y $（予測値）	65.411	71.849	78.288	81.507	87.945

Solution:

Step 1: 各データポイントの残差を計算します。

$ x $	60	70	80	85	95
$ y $（実際の値）	70	65	70	95	85
$ \ hat y $（予測値）	65.411	71.849	78.288	81.507	87.945
$ e $（残差）	4.589	-6.849	-8.288	13.493	-2.945

Step 2: -残差プロットグラフを描画します。

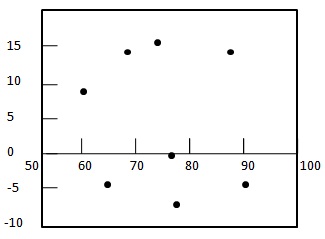
Step 3: -残差のランダム性を確認します。

ここで、残差プロットはランダムなパターンを示しています。最初の残余は正、次の2つは負、4つ目は正、最後の残余は負です。パターンは非常にランダムであるため、線形回帰モデルが上記のデータに適していることを示しています。