統計-F分布
F分布(SnedecorのF分布またはFisher-Snedecor分布)は、検定統計量のヌル分布として頻繁に発生する連続確率分布を表します。これは主に分散分析またはF検定中に発生します。
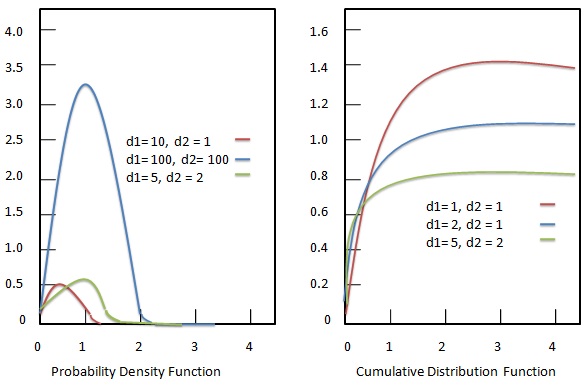
確率密度関数
F分布の確率密度関数は次のように与えられます。
式
$ {f(x; d_1、d_2)= \ frac {\ sqrt {\ frac {(d_1 x)^ {d_1} d_2 ^ {d_2}} {(d_1x + d_2)^ {d_1 + d_2}}}} { x \ beta(\ frac {d_1} {2}、\ frac {d_2} {2})}} $
ここで-
$ {d_1} $ =正のパラメーター。
$ {d_2} $ =正のパラメーター。
$ {x} $ =確率変数。
累積分布関数
F分布の累積分布関数は次のように与えられます。
式
$ {F(x; d_1、d_2)= I _ {\ frac {d_1x} {d_1x + d_2}}(\ frac {d_1} {2}、\ frac {d_2} {2})} $
ここで-
$ {d_1} $ =正のパラメーター。
$ {d_2} $ =正のパラメーター。
$ {x} $ =確率変数。
$ {I} $ =より低い不完全ベータ関数。