Estatísticas - Tabela Chi Quadrado

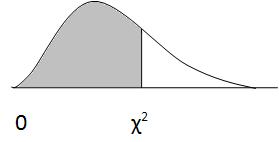
Os números na tabela representam os valores das estatísticas $ {\ chi ^ 2} $. As áreas da região sombreada (A) são os índices da coluna. Você também pode usar a distribuição qui-quadrado para calcular os valores críticos ep exatamente.

df	A = 0,005	0,010	0,025	0,05	0,10	0,25	0,50	0,75	0,90	0,95	0,975	0,99	0,995
1	0,000039	0,00016	0,00098	0,0039	0,0158	0,102	0,455	1,32	2,71	3,84	5.02	6,63	7,88
2	0,0100	0,0201	0,0506	0,103	0,211	0,575	1,39	2,77	4,61	5,99	7,38	9,21	10,6
3	0,0717	0,115	0,216	0,352	0,584	1,21	2,37	4,11	6,25	7,81	9,35	11,3	12,8
4	0,207	0,297	0,484	0,711	1.06	1,92	3,36	5,39	7,78	9,49	11,1	13,3	14,9
5	0,412	0,554	0,831	1,15	1,61	2,67	4,35	6,63	9,24	11,1	12,8	15,1	16,7
6	0,676	0,872	1,24	1,64	2,20	3,45	5,35	7,84	10,6	12,6	14,4	16,8	18,5
7	0,989	1,24	1,69	2,17	2,83	4,25	6,35	9,04	12,0	14,1	16,0	18,5	20,3
8	1,34	1,65	2,18	2,73	3,49	5.07	7,34	10,2	13,4	15,5	17,5	20,1	22,0
9	1,73	2.09	2,70	3,33	4,17	5,9	8,34	11,4	14,7	16,9	19,0	21,7	23,6
10	2,16	2,56	3,25	3,94	4,87	6,74	9,34	12,5	16,0	18,3	20,5	23,2	25,2
11	2,60	3,05	3,82	4,57	5,58	7,58	10,3	13,7	17,3	19,7	21,9	24,7	26,8
12	3,07	3,57	4,40	5,23	6,30	8,44	11,3	14,8	18,5	21,0	23,3	26,2	28,3
13	3,57	4,11	5.01	5,89	7,04	9,3	12,3	16,0	19,8	22,4	24,7	27,7	29,8
14	4,07	4,66	5,63	6,57	7,79	10,2	13,3	17,1	21,1	23,7	26,1	29,1	31,3
15	4,60	5,23	6,26	7,26	8,55	11,0	14,3	18,2	22,3	25,0	27,5	30,6	32,8
16	5,14	5,81	6,91	7,96	9,31	11,9	15,3	19,4	23,5	26,3	28,8	32,0	34,3
17	5,70	6,41	7,56	8,67	10,1	12,8	16,3	20,5	24,8	27,6	30,2	33,4	35,7
18	6,26	7,01	8,23	9,39	10,9	13,7	17,3	21,6	26,0	28,9	31,5	34,8	37,2
19	6,84	7,63	8,91	10,1	11,7	14,6	18,3	22,7	27,2	30,1	32,9	36,2	38,6
20	7,43	8,26	9,59	10,9	12,4	15,5	19,3	23,8	28,4	31,4	34,2	37,6	40,0
21	8.03	8,90	10,3	11,6	13,2	16,3	20,3	24,9	29,6	32,7	35,5	38,9	41,4
22	8,64	9,54	11,0	12,3	14,0	17,2	21,3	26,0	30,8	33,9	36,8	40,3	42,8
23	9,26	10,2	11,7	13,1	14,8	18,1	22,3	27,1	32,0	35,2	38,1	41,6	44,2
24	9,89	10,9	12,4	13,8	15,7	19,0	23,3	28,2	33,2	36,4	39,4	43,0	45,6
25	10,5	11,5	13,1	14,6	16,5	19,9	24,3	29,3	34,4	37,7	40,6	44,3	46,9
26	11,2	12,2	13,8	15,4	17,3	20,8	25,3	30,4	35,6	38,9	41,9	45,6	48,3
27	11,8	12,9	14,6	16,2	18,1	21,7	26,3	31,5	36,7	40,1	43,2	47,0	49,6
28	12,5	13,6	15,3	16,9	18,9	22,7	27,3	32,6	37,9	41,3	44,5	48,3	51,0
29	13,1	14,3	16,0	17,7	19,8	23,6	28,3	33,7	39,1	42,6	45,7	49,6	52,3
30	13,8	15.0	16,8	18,5	20,6	24,5	29,3	34,8	40,3	43,8	47,0	50,9	53,7
31	14,5	15,7	17,5	19,3	21,4	25,4	30,3	35,9	41,4	45,0	48,2	52,2	55.0
32	15,1	16,4	18,3	20,1	22,3	26,3	31,3	37,0	42,6	46,2	49,5	53,5	56,3
33	15,8	17,1	19,0	20,9	23,1	27,2	32,3	38,1	43,7	47,4	50,7	54,8	57,6
34	16,5	17,8	19,8	21,7	24,0	28,1	33,3	39,1	44,9	48,6	52,0	56,1	59,0
35	17,2	18,5	20,6	22,5	24,8	29,1	34,3	40,2	46,1	49,8	53,2	57,3	60,3
36	17,9	19,2	21,3	23,3	25,6	30,0	35,3	41,3	47,2	51,0	54,4	58,6	61,6
37	18,6	20,0	22,1	24,1	26,5	30,9	36,3	42,4	48,4	52,2	55,7	59,9	62,9
38	19,3	20,7	22,9	24,9	27,3	31,8	37,3	43,5	49,5	53,4	56,9	61,2	64,2
39	20,0	21,4	23,7	25,7	28,2	32,7	38,3	44,5	50,7	54,6	58,1	62,4	65,5
40	20,7	22,2	24,4	26,5	29,1	33,7	39,3	45,6	51,8	55,8	59,3	63,7	66,8
41	21,4	22,9	25,2	27,3	29,9	34,6	40,3	46,7	52,9	56,9	60,6	65,0	68,1
42	22,1	23,7	26,0	28,1	30,8	35,5	41,3	47,8	54,1	58,1	61,8	66,2	69,3
43	22,9	24,4	26,8	29,0	31,6	36,4	42,3	48,8	55,2	59,3	63,0	67,5	70,6
44	23,6	25,1	27,6	29,8	32,5	37,4	43,3	49,9	56,4	60,5	64,2	68,7	71,9
45	24,3	25,9	28,4	30,6	33,4	38,3	44,3	51,0	57,5	61,7	65,4	70,0	73,2
df	A = 0,005	0,010	0,025	0,05	0,10	0,25	0,50	0,75	0,90	0,95	0,975	0,99	0,995