Estatísticas - Diagrama de Venn
O diagrama de Venn é uma forma de representar visualmente o relacionamento entre grupos de entidades ou objetos. Os diagramas de Venn são compostos de círculos onde cada círculo representa um conjunto completo. O diagrama de Venn pode ter círculos ilimitados, mas geralmente dois ou três círculos são preferidos, caso contrário, o diagrama se torna muito complexo.
Passos para desenhar um diagrama de Venn
Considere os seguintes conjuntos de pessoas:
Cricket Players - $ C = \ {Ram, Shyam, Mohan, Rohan, Ramesh, Suresh \} $
Hockey Players - $ H = \ {Ramesh, Naresh, Mahesh, Leela, Sunita \} $
Etapa 1: desenhe um retângulo e rotule-o como jogadores.
Etapa 2: desenhe dois círculos e rotule-os como Críquete e Hóquei. Certifique-se de que os círculos se sobreponham.
Etapa 3: escreva os nomes dentro do círculo conforme relevante. Os nomes comuns devem estar dentro da região comum.
União
Union ($ \ cup $) representa um conjunto onde os itens estão presentes em todas as categorias, mas não são repetidos.
Exemplo
Problem Statement:
Desenhe um diagrama de Venn de $ C \ xícara H $.
Solution:
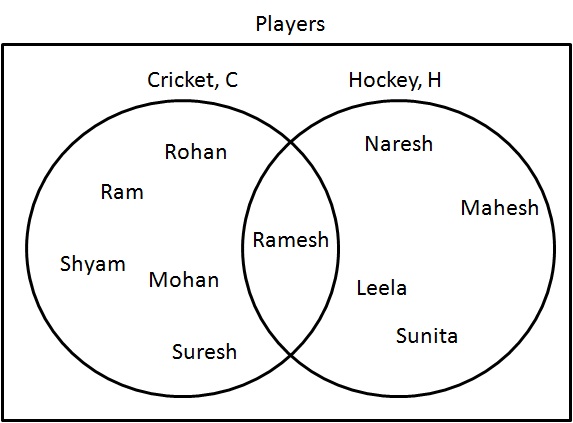
Etapa 1: determine os jogadores que estão jogando críquete ou hóquei. Desenhe-os da seguinte forma:
$ C \ cup H = \ {Ram, Shyam, Mohan, Rohan, Ramesh, Suresh, Naresh, Mahesh, Leela, Sunita \} $.

Interseção
A interseção ($ \ cap $) representa um conjunto onde os itens estão presentes em ambas as categorias.
Exemplo
Problem Statement:
Desenhe um diagrama de Venn de $ C \ cap H $.
Solution:
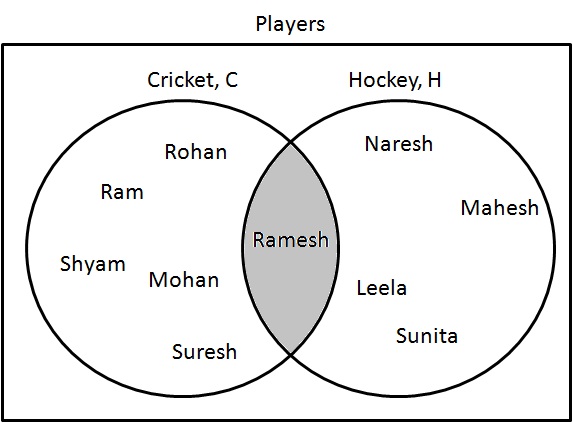
Etapa 1: determine os jogadores que estão jogando críquete e hóquei. Desenhe-os da seguinte forma:
$ C \ cap H = \ {Ramesh \} $.
Diferença
Diferença ($ - $) representa um conjunto onde os itens estão presentes apenas em uma categoria e não em outra.
Exemplo
Problem Statement:
Desenhe um diagrama de Venn de $ C - H $.
Solution:
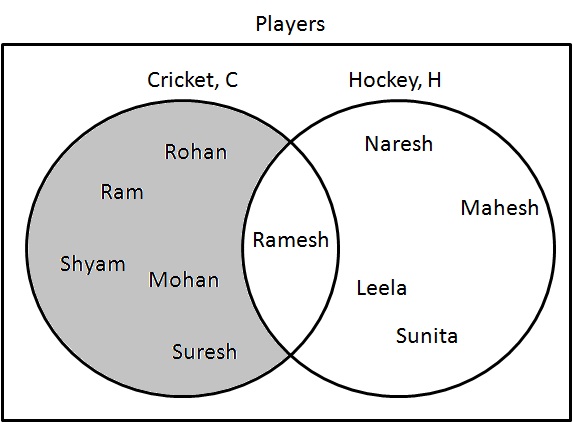
Etapa 1: determine os jogadores que estão jogando apenas críquete. Desenhe-os da seguinte forma:
$ C - H = \ {Ram, Shyam, Mohan, Rohan, Suresh \} $.