Estatísticas - distribuição exponencial
A distribuição exponencial ou distribuição exponencial negativa representa uma distribuição de probabilidade para descrever o tempo entre eventos em um processo de Poisson. No processo de Poisson, os eventos ocorrem de forma contínua e independente a uma taxa média constante. A distribuição exponencial é um caso particular da distribuição gama.
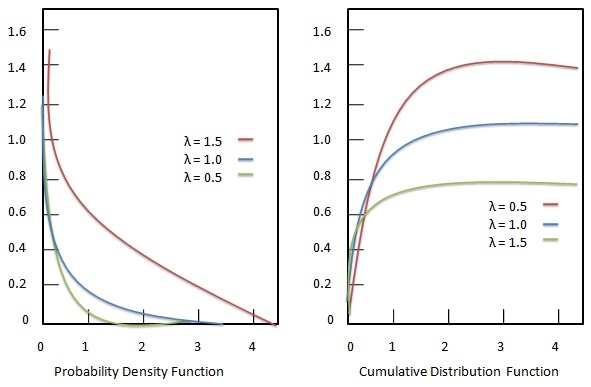
Função densidade de probabilidade
A função de densidade de probabilidade da distribuição exponencial é dada como:
Fórmula
$ {f (x; \ lambda) =} $ $ \ begin {casos} \ lambda e ^ {- \ lambda x}, & \ text {if $ x \ ge 0 $} \\ [7pt] 0, & \ texto {if $ x \ lt 0 $} \ end {cases} $
Onde -
$ {\ lambda} $ = parâmetro de taxa.
$ {x} $ = variável aleatória.
Função de distribuição cumulativa
A função de distribuição cumulativa da distribuição exponencial é dada como:
Fórmula
$ {F (x; \ lambda) =} $ $ \ begin {cases} 1- e ^ {- \ lambda x}, & \ text {if $ x \ ge 0 $} \\ [7pt] 0, & \ texto {if $ x \ lt 0 $} \ end {cases} $
Onde -
$ {\ lambda} $ = parâmetro de taxa.
$ {x} $ = variável aleatória.