Estatísticas - Comparando gráficos
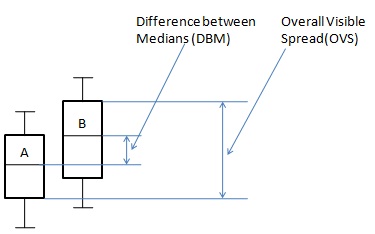
Os grupos da população podem ser comparados usando gráficos de caixa e bigode. A propagação visível geral e a diferença entre a mediana são usadas para chegar à conclusão de que tende a haver uma diferença entre dois grupos ou não.
Caso 2: Fórmula
$ {P = \ frac {DBM} {OVS} \ vezes 100} $
Onde -
$ {P} $ = diferença percentual
$ {DBM} $ = diferença entre medianas.
$ {OVS} $ = Spread Visível Geral.
Regras
Para um tamanho de amostra de 30, se essa porcentagem for maior que 33%, tende a haver uma diferença entre os dois grupos.
Para um tamanho de amostra de 100, se essa porcentagem for maior que 20%, tende a haver uma diferença entre os dois grupos.
Para um tamanho de amostra de 1000, se essa porcentagem for maior que 10%, tende a haver uma diferença entre os dois grupos.
Exemplo
Declaração do problema:
Descreva a diferença entre os seguintes conjuntos de dados.
| Sr. Não. | Nome | Conjunto A | Conjunto B |
|---|---|---|---|
| 1 | Max | 12 | 15 |
| 2 | UQ | 10 | 13 |
| 3 | Mediana | 7 | 10 |
| 4 | LQ | 6 | 9 |
| 5 | Min | 5 | 6 |
Solução:
Considere o seguinte diagrama:
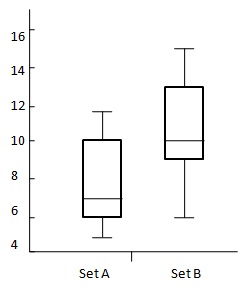
$ {OVS = 13 - 6 \\ [7pt] \ = 7 \\ [7pt] \ DBM = 10 -3 \\ [7pt] \ = 4} $
Aplicar a fórmula
$ {P = \ frac {DBM} {OVS} \ vezes 100 \\ [7pt] \ = \ frac {4} {7} \ vezes 100 \\ [7pt] \ = 57,14} $
Como a porcentagem é superior a 33%, há uma diferença entre o Conjunto A e o Conjunto B. É provável que o Conjunto B seja maior do que o Conjunto A.