Estatísticas - distribuição F
A distribuição F (distribuição F de Snedecor ou distribuição de Fisher-Snedecor) representa a distribuição de probabilidade contínua que ocorre freqüentemente como distribuição nula de estatísticas de teste. Isso acontece principalmente durante a análise de variância ou teste F.
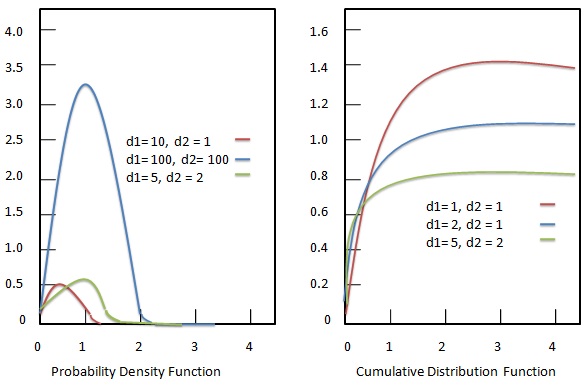
Função densidade de probabilidade
A função de densidade de probabilidade da distribuição F é dada como:
Fórmula
Onde -
$ {d_1} $ = parâmetro positivo.
$ {d_2} $ = parâmetro positivo.
$ {x} $ = variável aleatória.
Função de distribuição cumulativa
A função de distribuição cumulativa da distribuição F é dada como:
Fórmula
$ {F (x; d_1, d_2) = I _ {\ frac {d_1x} {d_1x + d_2}} (\ frac {d_1} {2}, \ frac {d_2} {2})} $
Onde -
$ {d_1} $ = parâmetro positivo.
$ {d_2} $ = parâmetro positivo.
$ {x} $ = variável aleatória.
$ {I} $ = função beta incompleta inferior.